Binomialverteilung
Binomialverteilung Definition
Die Binomialverteilung ist eine der diskreten Wahrscheinlichkeitsverteilungen.
Mit ihr kann man folgende Frage beantworten: wie hoch ist die Wahrscheinlichkeit, dass bei n-maliger Wiederholung eines Zufallsexperiments genau m "Erfolge" (d.h. das Ergebnis, für das man sich interessiert) auftreten?
Beispiel
Wie hoch ist die Wahrscheinlichkeit, dass bei einem 5-maligen Münzwurf genau 3 mal "Zahl" kommt?
Die Berechnung erfolgt mit der Formel (mit p als Wahrscheinlichkeit für den "Erfolg"):
n! / [ m! × (n - m)! ] × pm × (1 - p)n - m
Der erste Teil der Formel – n! / [ m! × (n - m)! ] – ist der Binomialkoeffizient B (n über m), der sich mit dem Taschenrechner berechnen lässt.
Die Binomialverteilung ergibt sich, wenn ein Bernoulli-Experiment mehrmals durchgeführt wird, setzt also voraus,
- dass das Experiment nur 2 mögliche Ergebnisse haben kann (z.B. Kopf oder Zahl, gerade oder ungerade, bestanden oder durchgefallen, etc.) und
- dass die Wahrscheinlichkeit für die 2 Ergebnisse bei jeder Durchführung konstant bleibt ("Ziehen mit Zurücklegen") und die Ergebnisse unabhängig voneinander sind (das Ergebnis der 1. Versuchsdurchführung wirkt sich nicht auf die 2. Versuchsdurchführung aus).
Beispiel
Beispiel: Binomialverteilung berechnen
Die Wahrscheinlichkeit für 3 mal "Zahl" bei 5-maligem Münzwurf berechnet sich mit folgender Formel:
{ 5! / [ 3! × (5 - 3)! ] } × 0,5 3 × (1 - 0,5) (5 -3)
= { (5 × 4 × 3 × 2 × 1) / [ (3 × 2 × 1) × (2 × 1) ] } × 0,125 × 0,25
= 10 × 0,125 × 0,25 = 0,3125 (gut 31 %).
In der Formel ist ! das Zeichen für Fakultät, 0,5 die Wahrscheinlichkeit für "Zahl" sowie (1 - 0,5) die Gegenwahrscheinlichkeit (die Wahrscheinlichkeit, dass nicht "Zahl" sondern "Kopf" kommt).
Binomialverteilung
Die errechneten ca. 31 % sind nur ein Ergebnis; die eigentliche (Binomial-)Verteilung erhält man, wenn man die Berechnung für 0 mal "Zahl", 1 mal "Zahl", 2 mal "Zahl", 3 mal "Zahl", 4 mal "Zahl" und 5 mal "Zahl" durchführt (hier inkl. der kumulierten Binomialverteilung, die z.B. angibt, dass die Wahrscheinlichkeit, maximal 2 mal Zahl zu erhalten – d.h., 0 mal "Zahl" oder 1 mal "Zahl" oder 2 mal "Zahl" –, 0,5 bzw. 50 % ist):
| Wahrscheinlichkeit | kumulierte Wahrscheinlichkeit | |
|---|---|---|
| 0 mal Zahl | 0,03125 | 0,03125 |
| 1 mal Zahl | 0,15625 | 0,1875 |
| 2 mal Zahl | 0,3125 | 0,5 |
| 3 mal Zahl | 0,3125 | 0,8125 |
| 4 mal Zahl | 0,15625 | 0,96875 |
| 5 mal Zahl | 0,03125 | 1 |
Die 5 Ergebnisse kann man auch in einer Grafik (z.B. Stabdiagramm) darstellen und man erhält dadurch die Abbildung einer Binomialverteilung. Da p = 0,5 ist, ist die Binomialverteilung symmetrisch (bei einem Würfel wäre es anders):
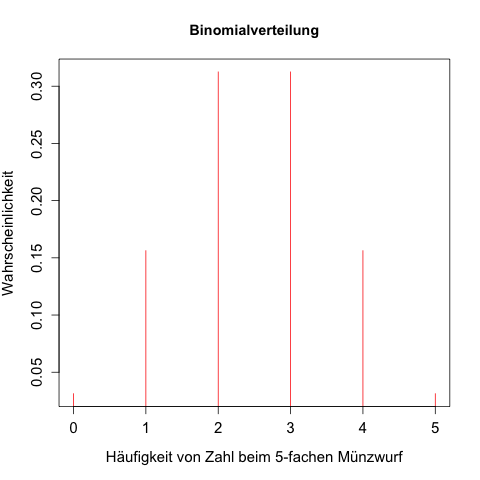
X ~ Bin (n, p) – im Beispiel Bin (5, 0,5) – besagt, dass die Zufallsvariable X ("Anzahl von Zahl") binomialverteilt ist mit n = 5 und Wahrscheinlichkeit p = 0,5.
Mindestens ... Erfolge
Ist nach der Wahrscheinlichkeit für z.B. mindestens 3 Erfolge gefragt, müssen die Wahrscheinlichkeiten für 3, 4 und 5 Erfolge aufaddiert werden: 0,3125 + 0,15625 + 0,03125 = 0,5.
Höchstens ... Erfolge
Wird nach der Wahrscheinlichkeit für z.B. höchstens 3 Erfolge gefragt, ist dies die Gegenwahrscheinlichkeit zu "mindestens 4 Erfolge": 1 - (0,15625 + 0,03125) = 1 - 0,1875 = 0,8125, ca. 81 %; alternativ kann es in der obigen Tabelle direkt in der Spalte für die kumulierte Wahrscheinlichkeit in der Zeile für "3 mal Zahl" abgelesen werden (die Summe der Wahrscheinlichkeiten für 0 mal, einmal, zweimal oder dreimal Zahl).
Erwartungswert Binomialverteilung
Der Erwartungswert einer Binomialverteilung entspricht dem Produkt aus der Anzahl der Durchführungen des Bernoulli-Experiments und der (Erfolgs-)Wahrscheinlichkeit (als Formel: Erwartungswert = n × p mit n als Anzahl der Experimentsdurchführungen und p als Erfolgswahrscheinlichkeit).
Beispiel
Der Erwartungswert für "Zahl" bei 5-maligem Münzwurf ist: 5 × 0,5 = 2,5.
Das Ergebnis – 2,5 – ist etwas schlecht vorstellbar bzw. interpretierbar. Klarer wird es, wenn man z.B. mit 10 oder 50 Würfen rechnet: bei 10 Münzwürfen ist 5 mal "Zahl" zu erwarten (10 × 0,5 = 5), bei 50 Würfen 25 mal "Zahl" (50 × 0,5 = 25) u.s.w.
Varianz / Standardabweichung Binomialverteilung
Die Varianz einer Binomialverteilung entspricht dem Produkt aus dem Erwartungswert und der Misserfolgswahrscheinlichkeit (der Gegenwahrscheinlichkeit zum "Erfolg").
Als Formel: Varianz = n × p × (1 - p) mit n als Anzahl der Experimentsdurchführungen, p als Erfolgswahrscheinlichkeit und (1 - p) als Gegen- bzw. Mißerfolgswahrscheinlichkeit.
Beispiel
Die Varianz für das obige Beispiel ist: 2,5 × 0,5 = 1,25.
Dabei ist 2,5 der oben berechnete Erwartungswert (Anzahl der Durchführungen bzw. Münzwürfe mal die Wahrscheinlichkeit für "Zahl") und 0,5 ist die Misserfolgswahrscheinlichkeit (die Wahrscheinlichkeit, dass nicht "Zahl", sondern "Kopf" kommt).
Standardabweichung
Die Standardabweichung ist die Quadratwurzel der Varianz, d.h. die Wurzel aus 1,25 = 1,118.
Approximation durch Normalverteilung
Die Binomialverteilung kann durch die Normalverteilung approximiert werden, wenn sowohl n × p (der Erwartungswert) als auch n × (1 - p) mindestens 10 betragen.
Im obigen Beispiel ist n × p = 5 × 0,5 = 2,5, damit ist schon die erste Bedingung nicht erfüllt.
Wäre die Anzahl der Versuchsdurchführungen 20 oder mehr, könnte die Normal-Approximation hier durchgeführt werden.
Die für die Normalverteilung anzuwendenden Parameter wären dann:
- Erwartungswert = 20 × 0,5 = 10;
- Varianz = 10 × (1 - 0,5) = 5; die Standardabweichung als Wurzel der Varianz wäre dann 2,236.