Geometrische Verteilung
Geometrische Verteilung Definition
Die geometrische Verteilung ist eine Art der diskreten Verteilungen.
Sie bezieht sich auf die Anzahl der Durchführungen bis zum ersten "Erfolg". Dabei kann der Erfolg zum Beispiel eine 6 beim Würfeln, Zahl beim Münzwurf oder Rot beim Roulette sein ("Erfolg" ist also das Ergebnis, für das man sich interessiert).
Die geometrische Verteilung basiert auf Bernoulli-Experimenten, für die die Wahrscheinlichkeit eines "Erfolgs" bekannt ist (oder zumindest geschätzt werden kann).
Beispiel 1
Aus einem Set mit Skatkarten werden die 4 Könige (Karo, Herz, Pik und Kreuz) entnommen. Spieler 1 mischt die 4 Karten und Spieler 2 muss verdeckt eine ziehen, solange bis er den Kreuz König (den "Erfolg") hat; wenn er eine andere "falsche" Karte zieht, muss er diese wieder zurückgeben und sie wird mit den anderen wieder gemischt.
Wie hoch ist die Wahrscheinlichkeit, dass der Spieler 2 erst beim 3. Versuch den Kreuz König zieht?
Die Wahrscheinlichkeit beim verdeckten Ziehen ist hier für jede Karte 1/4 = 25 %. Die Wahrscheinlichkeit, erst beim 3. Versuch den Kreuz König zu ziehen, ist (1 - 0,25)(3 - 1) × 0,25 = 0,752 × 0,25 = 0,5625 × 0,25 = 0,140625 (gerundet ca. 14 %).
Wie lässt sich das herleiten? Um erst beim 3. Versuch den Erfolg zu erzielen, müssen die ersten beiden Versuche Mißerfolge sein (das heißt Karo, Herz oder Pik König) und der 3. Versuch ein Erfolg (Kreuz König). Die Wahrscheinlichkeit für einen Misserfolg (die Gegenwahrscheinlichkeit) beim 1. Versuch ist 75 % , beim 2. Versuch ebenso 75 % und die Wahrscheinlichkeit beim 3. Versuch für einen Erfolg ist 25 %; das ergibt 0,75 × 0,75 × 0,25 = 0,140625.
Allgemein als Formel: die Wahrscheinlichkeit, erst beim n-ten Versuch einen Erfolg zu erzielen ist: Gegenwahrscheinlichkeit (n -1) × Erfolgswahrscheinlichkeit (oder mit vertauschten Faktoren: Erfolgswahrscheinlichkeit × Gegenwahrscheinlichkeit(n -1)).
Beispiel 2
Man darf bei einem Brettspiel erst mitspielen, wenn man eine 6 gewürfelt hat. Wie hoch ist die Wahrscheinlichkeit, erst nach 3-maligem Würfeln mitspielen zu dürfen?
Die Wahrscheinlichkeit, eine 6 zu würfeln ist 1/6, die Gegenwahrscheinlichkeit (das heißt, man würfelt eine 1, 2, 3, 4 oder 5) ist 5/6.
In die Formel eingesetzt: 5/6(3 - 1) × 1/6 = 5/62 × 1/6 = 0,11574 (gerundet knapp 11,6 %).
Verteilung
In den obigen Beispielen wurde eine einzelne bestimmte Wahrscheinlichkeit berechnet. Die eigentliche geometrische Verteilung umfasst jedoch mehrere Wahrscheinlichkeiten, eben die Verteilung der Wahrscheinlichkeiten.
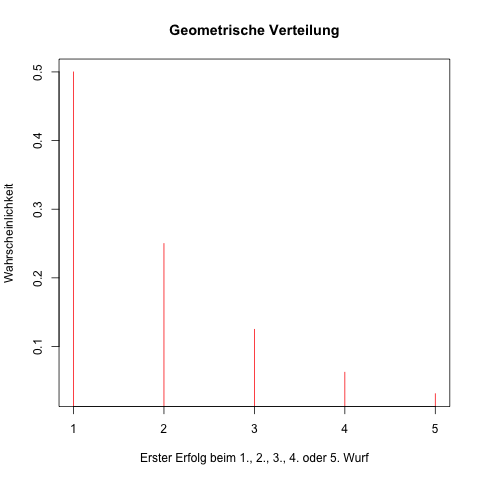
Beispiel: Geometrische Verteilung beim Münzwurf
Die geometrische Wahrscheinlichkeit, beim k-ten Münzwurf erstmalig "Kopf" zu erhalten, ist für 5 Münzwürfe wie folgt:
- P (X = 1) = 1/2 = 0,5 (X = 1 bedeutet: "Kopf" beim 1. Wurf; hier gibt es nur den einen Wurf)
- P (X = 2) = 1/2 × 1/2(2-1) = 1/4 = 0,25 (X = 2 bedeutet: "Kopf" erstmalig beim 2. Wurf)
- P (X = 3) = 1/2 × 1/2(3-1) = 1/8 = 0,125 (X = 3 bedeutet: "Kopf" erstmalig beim 3. Wurf)
- P (X = 4) = 1/2 × 1/2(4-1) = 1/16 = 0,0625
- P (X = 5) = 1/2 × 1/2(5-1) = 1/32 = 0,03125
Es ist also mit ca. 3 % schon ziemlich unwahrscheinlich, erst beim 5. Wurf "Kopf" zu erhalten.
Als Grafik:
Erwartungswert und Varianz der geometrischen Verteilung
Der Erwartungswert einer geometrischen Verteilung gibt an, wie lange man im Mittel auf den ersten Erfolg warten muss, im Beispiel: wie oft muss man die Münze werfen, bis erstmalig "Kopf" kommt.
Der Erwartungswert ist 1/p (mit p für Wahrscheinlichkeit) = 1 / 0,5 = 2 (2. Wurf).
Die Varianz einer geometrischen Verteilung ist (1 - p) / p2 = 0,5 / 0,25 = 2.