Hypothesentest
Hypothesentest Definition
Eine Hypothese ist eine Vermutung oder Annahme bzgl. eines bestimmten quantifizierbaren Sachverhalts bzw. Parameters einer Grundgesamtheit (z.B. "5 % der Produktionsmenge sind defekt"); durch den Hypothesentest soll die Vermutung auf Basis einer Stichprobe bestätigt oder widerlegt werden.
Die Bestätigung ist jedoch kein Beweis, dass die Hypothese stimmt; es gibt lediglich eine (ggfs. hohe) Wahrscheinlichkeit, dass die Hypothese stimmt (vgl. Fehler 1. und 2. Art).
Alternative Begriffe: Hypothesenprüfung, Signifikanzprüfung, Signifikanztest, statistischer Test.
Beispiel
Hypothesentest Beispiel
Ein Schiedsrichter übt vor dem Spiel 5 Minuten lang Münzwurf. Er hat das Gefühl, dass mit der Münze etwas nicht stimmt, es kommt sehr häufig Kopf und nur selten Zahl.
Er möchte das statistisch mit einer Stichprobe von 10 Würfen untersuchen und stellt folgende Hypothesen auf:
- sog. Nullhypothese: Wahrscheinlichkeit für Kopf = 0,5 bzw. 50 % (das wäre eine korrekte, faire Münze);
- sog. Alternativhypothese: Wahrscheinlichkeit für Kopf ungleich 0,5 bzw. 50 % (dann wäre die Münze nicht in Ordnung bzw. "defekt").
Zudem legt er ein sog. Signifikanzniveau (eine Art Fehlertoleranz) mit 0,05 bzw. 5 % fest.
Damit handelt es sich um einen sog. zweiseitigen Signifikanztest.
Der Schiedsrichter wirft die Münze 10 mal (besser wären 100 oder 1.000 mal) und notiert, wie oft Kopf kommt: 7 mal; eigentlich würde man bei 10 Münzwürfen 5 mal Kopf erwarten. Die Anzahl von Kopf ist hier die sog. Teststatistik bzw. Prüfgröße, anhand derer dann die Testentscheidung getroffen wird.
Ist die Münze "defekt" oder ist das nur eine zufällige Abweichung?
In der folgenden Tabelle sind die mit der Formel für die Binomialverteilung berechneten Wahrscheinlichkeiten für 0 mal Kopf, 1 mal Kopf etc. und die kumulierten Wahrscheinlichkeiten (z.B. maximal 1 mal Kopf ist die Summe der Wahrscheinlichkeiten für 0 mal Kopf und 1 mal Kopf) dargestellt.
| Wahrscheinlichkeit | kumulierte Wahrscheinlichkeit | |
|---|---|---|
| 0 mal Kopf | 0,0009765625 | 0,0009765625 |
| 1 mal Kopf | 0,009765625 | 0,0107421875 |
| 2 mal Kopf | 0,0439453125 | 0,0546875 |
| 3 mal Kopf | 0,1171875 | 0,171875 |
| 4 mal Kopf | 0,205078125 | 0,376953125 |
| 5 mal Kopf | 0,24609375 | 0,623046875 |
| 6 mal Kopf | 0,205078125 | 0,828125 |
| 7 mal Kopf | 0,1171875 | 0,9453125 | 8 mal Kopf | 0,0439453125 | 0,9892578125 |
| 9 mal Kopf | 0,009765625 | 0,9990234375 |
| 10 mal Kopf | 0,0009765625 | 1 |
Beispiel: die Wahrscheinlichkeit, bei 10 Münzwürfen 2 mal Kopf zu erhalten ist 0,0439453125, also ca. 4,4 %; die Wahrscheinlichkeit, bei 10 Würfen maximal 2 mal Kopf zu erhalten ist 0,0546875 bzw. ca. 5,5 % (die aufaddierte Wahrscheinlichkeit für 0 mal Kopf, 1 mal Kopf und 2 mal Kopf).
Ablehnungsbereich
Für die Nullhypothese gibt es nun einen sog. Ablehnungsbereich – Häufigkeiten von Kopf, die sehr unwahrscheinlich sind –, der von der Höhe des Signifikanzniveaus abhängt.
Die Wahrscheinlichkeit, dass zwischen 2 und 8 mal Kopf kommt, ist 0,978515625 bzw. gerundet 97,9 % (Summe der jeweiligen Wahrscheinlichkeiten oder kürzer: kumulierte Wahrscheinlichkeit für 8 mal Kopf minus kumulierte Wahrscheinlichkeit für 1 mal Kopf = 0,9892578125 - 0,0107421875 = 0,978515625); die Wahrscheinlichkeit, dass 0 mal, 1 mal, 9 mal oder 10 mal Kopf kommt, ist der Rest, d.h. ca. 2,1 % (sehr unwahrscheinlich); für diese Fälle würde der Schiedsrichter die Nullhypothese (Münze ist fair) ablehnen; es kam aber 7 mal Kopf, dies ist im 97,9 % - Intervall, damit wird die Nullhypothese nicht abgelehnt und er wird die Münze als fair betrachten und im Spiel benutzen.
Der Ablehnungsbereich umfasst also 0, 1, 9 und 10 mal Kopf, der sog. Annahmebereich (bei dem die Nullhypothese angenommen wird) umfasst 2 bis 8 mal Kopf — und da die Teststatistik mit 7 nicht im Ablehnungsbereich liegt, wird die Nullhypothese bei diesem Signifikanzniveau nicht verworfen.
Ablehnungsbereich (rot) und Annahmebereich (grün) in einer Grafik dargestellt:
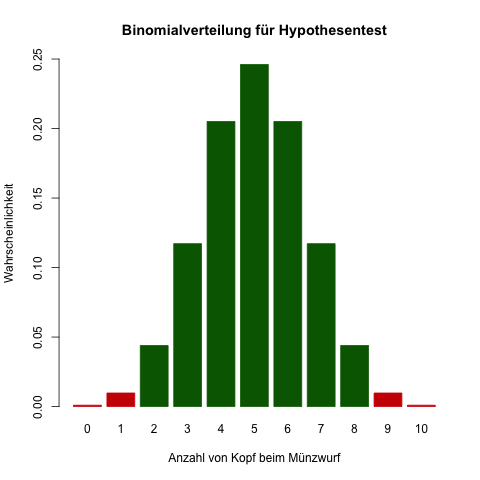
Wäre z.B. 9 mal oder 10 mal Kopf gekommen, hätte der Schiedsrichter die Nullhypothese abgelehnt und die Münze für "defekt" erklärt — in der Tabelle sieht man, dass 9 mal Kopf oder 10 mal Kopf mit 0,009765625 + 0,0009765625 = 0,010742187, also rund 1,1 % sehr unwahrscheinlich ist, aber im Bereich des Möglichen; absolut sicher kann man sich also auch bei diesem Ergebnis nicht sein, dass die Nullhypothese (Münze ist fair) nicht doch stimmt, aber zumindest ziemlich sicher (> 95 %).
In dem Beispiel handelt es sich um einen sog. zweiseitigen Hypothesentest: wir interessieren uns sowohl dafür, dass zu wenig häufig Kopf kommt als auch dafür, dass zu oft Kopf kommt (die Münze soll fair sein); bei anderen Fragestellungen interessiert ggfs. nur, ob etwas zu klein, zu wenig, zu jung etc. oder zu groß, zu viel, zu alt etc. ist (sog. einseitiger Hypothesentest).