Lineare Regression
Lineare Regression Definition
Die lineare Regression ist die relevanteste Form der Regressionsanalyse.
Die lineare Regression untersucht einen linearen Zusammenhang zwischen einer sog. abhängigen Variablen und einer unabhängigen Variablen (bivariate Regression) und bildet diesen Zusammenhang mit einer linearen Funktion yi = α + β × xi (mit α als Achsenabschnitt und β als Steigung der Geraden) bzw. Regressionsgeraden ab.
Um zu prüfen, ob die lineare Regression anwendbar ist, kann man die 2 Variablen mit ihren Messwerten zunächst in einem Streudiagramm eintragen. Liegen die Messwerte annähernd auf einer Geraden, kann eine lineare Regressionsanalyse vorgenommen werden.
Alternative Begriffe: Ausgleichsgerade, einfache lineare Regression, lineare Regressionsanalyse, lineares Regressionsmodell.
Beispiel
Beispiel Lineare Regression
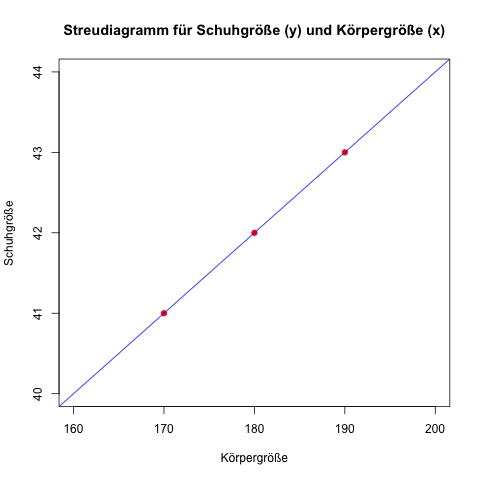
Für 3 Männer (Anton, Bernd und Claus) wird die Körpergröße in cm sowie die Schuhgröße erfasst. Gibt es einen linearen Zusammenhang? – und wie lässt sich dieser in einer Formel ausdrücken? In dem Fall soll die Schuhgröße (Variable y) aus der Körpergröße (Variable x) abgeleitet bzw. prognostiziert werden.
| Person | Körper-größe in cm (xi) | Schuh-größe (yi) | Abweichung der Körpergröße vom Mittelwert (xi - ∅x) | Quadrierte Abweichung der Körpergröße (xi - ∅x)2 | Abweichung der Schuhgröße vom Mittelwert (yi - ∅y) | Abweichung Körpergröße × Abweichung Schuhgröße (xi - ∅x) × (yi - ∅y) |
|---|---|---|---|---|---|---|
| Anton | 170 | 41 | -10 | 100 | -1 | 10 |
| Bernd | 180 | 42 | 0 | 0 | 0 | 0 |
| Claus | 190 | 43 | 10 | 100 | 1 | 10 |
| Summe | 200 | 20 |
Zunächst werden die arithmetischen Mittelwerte (Durchschnitte) für Körpergröße und Schuhgröße berechnet:
- Körpergröße: (170 cm + 180 cm + 190 cm) / 3 = 180 cm.
- Schuhgrösse: (41 + 42 + 43) / 3 = 126 / 3 = 42.
Anschließend werden (in den Spalten der Tabelle)
- für die Körpergröße die jeweiligen Abweichungen vom Mittelwert berechnet
- die Abweichung der Körpergröße wird quadriert
- für die Schuhgröße die jeweiligen Abweichungen vom Mittelwert berechnet und
- die Abweichungen vom Mittelwert jeweils multipliziert.
Steigung berechnen
Nun wird die Summe der multiplizierten Abweichungen durch die Summe der quadrierten Abweichungen der Körpergröße geteilt: 20 / 200 = 0,1.
Als Formel: β = ∑ [(xi - ∅x) × (yi - ∅y)] / ∑(xi - ∅x)2
Die so ermittelte Steigung der Regressionsgeraden entspricht dem Quotienten aus der Kovarianz (20/3) und der Varianz der Körpergröße (200/3).
Achsenabschnitt berechnen
Als letzter Schritt wird vom Durchschnitt der Schuhgröße der soeben berechnete Wert mal der Durchschnitt der Körpergröße abgezogen: 42 - 0,10 × 180 = 24.
Als Formel: α = ∅y - β × ∅x
Regressionsgerade
Die Regressionsgerade als lineare Funktion ist dann: 24 + 0,1 × Körpergröße.
Allgemein als Formel:
yi = α + β × xi
Dabei ist α (24) der Schnittpunkt mit der y-Achse (die Schuhgrößen fangen im Beispiel somit bei 24 an, bei der theoretischen Körpergröße 0), β (0,1) ist die Steigung der Regressionsgeraden und xi bzw. yi sind die jeweiligen Körper- und Schuhgrößen.
Dabei werden α und β auch als Regressionskoeffizienten bezeichnet bzw. α als Regressionskonstante; ß gibt an, um wie viele Einheiten y steigt, wenn x um eine Einheit steigt (im Beispiel: steigt die Körpergröße um 1 cm, steigt die Schuhgröße um 0,1 Schuhgrößen).
Für Anton: 24 + 0,1 × 170 = 41.
Für Bernd: 24 + 0,1 × 180 = 42.
Für Claus: 24 + 0,1 × 190 = 43.
Die Regressionsformel kann nun genutzt werden, um (für andere Männer) auf Basis einer Körpergröße eine Schätzung bzw. Prognose der Schuhgröße vorzunehmen.
Das Streudiagramm für die 3 Messdaten inkl. der Regressionsgeraden: