Lorenzkurve
Lorenzkurve Definition
Die Lorenzkurve misst wie der Gini-Koeffizient die relative Konzentration, ist allerdings ein grafisches Konzentrationsmaß. Die Lorenzkurve zeigt an, wie ungleichmäßig und ggfs. "ungerecht" Vermögen, Einkommen, Umsätze etc. verteilt sind.
Auf der horizontalen x-Achse werden die kumulierten Anzahlen der statistischen Einheiten (z.B. Menschen oder Unternehmen) als Anteilswerte mit Werten zwischen 0 und 1 und auf der vertikalen y-Achse die kumulierten Merkmalsausprägungen / Messwerte (z.B. Vermögen oder Umsätze) als Anteilswerte mit Werten zwischen 0 und 1 abgetragen.
Beispiel
Beispiel Lorenzkurve
Angelehnt an die Beispieldaten zum Gini-Koeffizienten: es soll die Vermögenskonzentration der Bevölkerung – im Beispiel stehen stellvertretend dafür nur 3 Personen A, B und C – grafisch dargestellt werden.
Das Vermögen der 3 Personen ist:
- A: 300.000 €
- B: 100.000 €
- C: 600.000 €
Das Gesamtvermögen als Summe der 3 Werte ist 1.000.000 €.
Lorenzkurve berechnen
Zunächst werden die Daten für die Lorenzkurve berechnet. Dazu werden die Vermögen der Höhe nach (aufsteigend) sortiert und es werden die kumulierten Anteile der Menschen und der Vermögen berechnet:
| Person | Vermögen | Personenanteil kumuliert | Vermögen kumuliert | Vermögensanteil kumuliert |
|---|---|---|---|---|
| B | 100.000 € | 0,33 | 100.000 € | 0,1 |
| A | 300.000 € | 0,67 | 400.000 € | 0,4 |
| C | 600.000 € | 1,0 | 1.000.000 € | 1,0 |
Lorenzkurve zeichnen
Man zeichnet 3 Koordinaten ein: (0,33, 0,1), (0,67, 0,4) und (1,00, 1,00); d.h., ein Anteil von 0,33 bzw. 33 % der Menschen (hier ein Mensch aus 3) verfügt zusammen über 0,1 % des gesamten Vermögens (100.000 € von insgesamt 1.000.000 €), ein Anteil von 0,67 bzw. 67 % der Menschen (hier: 2 aus 3) verfügt kumuliert über 40 % des Vermögens und alle Menschen zusammen dann über 1.000.000 €; anschließend verbindet man die 3 Koordinaten vom Nullpunkt des Koordinatenkreuzes aus durch Linien.
Zudem wird eine diagonale Linie zwischen den Koordinaten (0,0 / 0,0) und (1,0 / 1,0) eingezeichnet. Wären die Messwerte vollständig gleichmäßig bzw. ausgewogen verteilt, würde die Lorenzkurve der Diagonalen entsprechen. Liegt die Lorenzkurve – wie hier – unterhalb der Diagonalen, spricht dies für eine ungleichmäßige Verteilung bzw. für eine entsprechende Konzentration der Vermögen. Je extremer die Lorenzkurve unterhalb der Diagonalen "durchhängt", desto ungleichmäßiger ist die Verteilung.
Die Lorenzkurve (mit den 3 Koordinaten als Knickpunkten) sieht so aus:
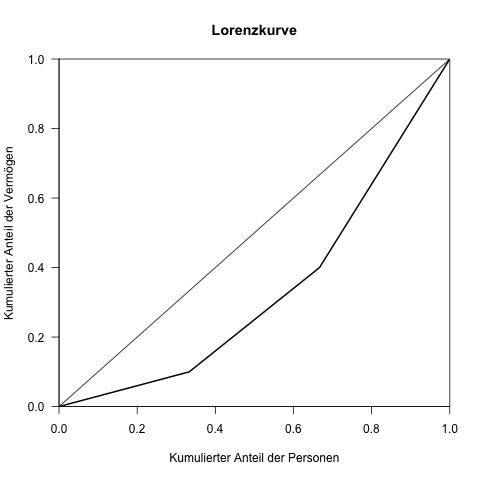
Dass das Vermögen in der Bevölkerung (hier: zwischen den 3 Personen) ungleichmäßig verteilt ist, sieht man hier auf den ersten Blick bereits an den wenigen Daten selbst; in der Realität sind aber natürlich viel mehr Daten abzubilden.