Betragsfunktion

Betragsfunktion Definition

Die Betragsfunktion ordnet einer Zahl dieselbe Zahl ohne (negatives) Vorzeichen zu; das Ergebnis – der Betrag einer Zahl oder Absolutbetrag – ist nie negativ.

Beispiel

Die Betragsfunktion f(x) = |x| ordnet der Zahl -5 die Zahl 5 zu; der Zahl 5 ordnet sie (ebenfalls) die Zahl 5 zu.

Negative Zahlen werden somit zu gleichhohen positiven Zahlen, während positive Zahlen (und die 0) unverändert bleiben.

Anwendung

Das kann man zum Beispiel bei der Messung von Abständen bzw. der Analyse von manchen Abweichungen gebrauchen.

Es kommt darauf an: teilweise sind positive und negative Abweichungen einfach Abstände vom Soll-Zustand und "gleich schlecht" (zum Beispiel wenn Schrauben zu kurz oder zu lang produziert sind) und es wird einfach die mittlere Abweichung zur Qualitätskontrolle berechnet.

Oft macht es aber einen Unterschied und man will zum Beispiel erfassen, ob die Umsätze positiv von der Planung abweichen (sehr schön) oder negativ (Maßnahmen sind zu ergreifen). Hier lässt man die Vorzeichen der Abweichungen und wendet die Betragsfunktion nicht an.

Grafisch

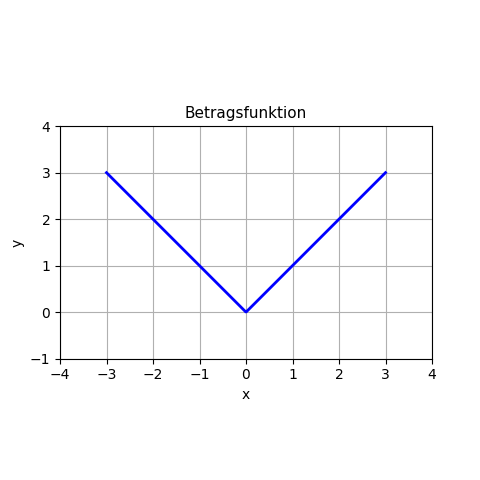
Die Betragsfunktion hat für x = 1 den Wert f(x) = 1, für x = 2 den Wert f(x) = 2 usw.

Und im negativen x-Bereich: für x = -1 den Wert f(x) = 1, für x = -2 den Wert f(x) = 2 usw.

Grafisch ergibt das ein „V“, dessen untere Spitze im Koordinatenursprung steht.

Besonderheiten: Nicht-Differenzbarkeit bei 0, Ableitung

Die Betragsfunktion hat ein paar Besonderheiten:

• Sie ist an der Stelle x = 0 nicht differenzierbar;
• Ihr Minimum ist bei x = 0 mit einem Funktionswert y = 0; dieser Tiefpunkt kann aber nicht wie üblich über das Gleichsetzen der 1. Ableitung mit 0 gefunden werden, da die 1. Ableitung bei 0 nicht existiert (nicht differenzierbar an der Stelle);
• Die 1. Ableitung der Betragsfunktion – die Steigung der Funktion – ist f’(x) = 1 für alle x > 0; und f’(x) = -1 für alle x < 0.