Methode der kleinsten Quadrate
Methode der kleinsten Quadrate Definition
Die lineare Regression basiert auf der von Carl Friedrich Gauß entwickelten Methode der kleinsten Quadrate.
Um die Ausgleichs- bzw. Regressionsgerade zu finden, die am besten zu den Datenpunkten passt, werden die quadrierten Abstände (Abstandsquadrate) zwischen den Datenpunkten (Messwerten) und der Regressionsfunktion/-geraden minimiert.
Das Quadrat der Abstände wird verwendet, um
- positive und negative Abweichungen gleich zu behandeln und um zu vermeiden, dass sich die Abweichungen gegenseitig aufheben (das könnte man auch durch die Verwendung absoluter Beträge erreichen) und um
- große Fehler stärker zu gewichten (12 = 1, 22 = 4, 32 = 9 und so weiter; die Verhältnisse ändern sich also nicht "nur" um 100 % (von 1 auf 2) bzw. 50 % (von 2 auf 3), sondern um 400 % (von 1 auf 4) bzw. um 225 % (von 4 auf 9)).
Alternative Begriffe: Kleinste-Quadrate-Methode, KQ-Methode, Methode der kleinsten Fehlerquadrate.
Beispiel
Beispiel: Methode der kleinsten Quadrate
Um diese Abstände zu zeigen, werden die Beispieldaten zur linearen Regression bezüglich der Schuhgröße etwas abgeändert (da diese zu schön sind, das heißt perfekt auf einer Linie liegen – und damit existieren keine Differenzen).
| Person | Körpergröße in cm (xi) | Schuhgröße (yi) |
|---|---|---|
| Anton | 170 | 42 |
| Bernd | 180 | 44 |
| Claus | 190 | 43 |
Das Streudiagramm für die 3 Messdaten inklusive der Regressionsgeraden (mit der auf den abgeänderten Daten basierenden Funktion: yi = α + β × xi = 34 + 0,05 × xi):
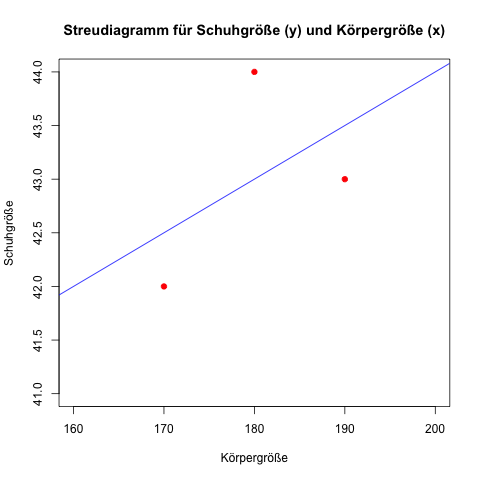
Anton hat eine Schuhgröße von 42, die lineare Regressionsfunktion berechnet für ihn einen "theoretischen" Wert von 34 + 0,05 × 170 = 42,5 (bei 170 cm Körpergröße geht die Gerade durch den y-Wert (Schuhgröße) 42,5).
Die "vertikalen Differenzen" zwischen den tatsächlichen (gemessenen) Werten und den theoretischen (berechneten) Werten auf der Regressionsgeraden sind die sogenannten Residuen, hier für Anton 42 - 42,5 = -0,5.
Die Berechnungen analog für Bernd: 34 + 0,05 × 180 = 43; das Residuum ist 44 - 43 = 1,0.
Und für Claus: 34 + 0,05 × 190 = 43,5; das Residuum ist 43 - 43,5 = -0,5.
Laut der Methode der kleinsten Quadrate ist die am beste passende Ausgleichsgerade diejenige, die die Summe der quadrierten Abstände für alle Datenpunkte minimiert.
Das ist die oben eingezeichnete Linie, die analog dem Beispiel zur linearen Regression berechnet wurde.
Wie gut die so gefundene Gerade passt, kann mit dem sogenannte Bestimmtheitsmaß gemessen und in einem Wert ausgedrückt werden (man sieht in der obigen Grafik, dass sie nicht sehr gut passen kann, da die Datenpunkte ziemlich weit von der Geraden entfernt sind).