Baumdiagramm
Baumdiagramm Definition
Mit einem Baumdiagramm können mehrstufige Zufallsexperimente (zum Beispiel zweimaliges Ziehen aus einer Urne) dargestellt und deren Wahrscheinlichkeiten berechnet werden. Es stellt alle möglichen Verzweigungen dar.
Für das Baumdiagramm gelten sogenannte Pfadregeln:
- 1. Pfadregel (Produktregel, Pfadmultiplikationsregel): Die Wahrscheinlichkeit eines Elementarereignisses ergibt sich, indem man die Wahrscheinlichkeiten der Teilpfade multipliziert.
- 2. Pfadregel (Summenregel, Pfadadditionsregel): Die Wahrscheinlichkeit eines Ereignisses ergibt sich, indem man die Wahrscheinlichkeiten der Elementarereignisse am Ende der Teilpfade addiert.
Bei jeder Verzweigung des Baumdiagramms ist die Summe aller Wahrscheinlichkeiten = 1 (sonst hat man einen Fehler gemacht).
Alternative Begriffe: Wahrscheinlichkeitsbaum.
Beispiel
Beispiel: Wahrscheinlichkeiten mit Baumdiagramm berechnen
In einer Urne / Trommel sind 3 rote und 4 schwarze Kugeln.
Es wird mit verbundenen Augen eine Kugel gezogen und auf den Tisch gelegt, dann wird noch eine zweite Kugel gezogen und auf den Tisch gelegt (das ist ein zweistufiges Zufallsexperiment ohne Zurücklegen).
Aufgabe / Frage
Wie hoch ist die Wahrscheinlichkeit, dass die beiden Kugeln auf dem Tisch dieselbe Farbe haben (also 2 mal rot oder 2 mal schwarz)?
Baumdiagramm zeichnen
Das Baumdiagramm kann senkrecht nach unten gehen mit linken und rechten Verzweigungen (wie in der Grafik unten) oder waagrecht nach rechts mit oberen und unteren Verzweigungen.
Die jeweiligen Möglichkeiten (rot und schwarz) stehen jeweils am Ende vom Zweig, auf den Zweigen selbst werden die Wahrscheinlichkeiten notiert.
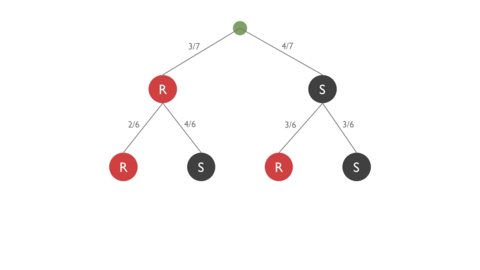
1. Pfad
Die 1. Verzweigung in dem Baumdiagramm wäre: links rot mit einer Wahrscheinlichkeit von 3/7, rechts schwarz mit einer Wahrscheinlichkeit von 4/7.
Wird im 1. Durchgang eine rote Kugel gezogen, sind noch 6 Kugeln übrig: 2 rote und 4 schwarze. Das gibt zwei neue Verzweigungen: links rot mit einer Wahrscheinlichkeit von 2/6 und rechts schwarz mit einer Wahrscheinlichkeit von 4/6.
Die Wahrscheinlichkeit, dass auf diesem Weg durch den Baum zweimal rot gezogen wird, ist nach der Pfadmultiplikationsregel: 3/7 × 2/6 = 6/42 = 1/7 (ca. 14,3 %).
2. Pfad
Wird im 1. Durchgang eine schwarze Kugel gezogen (mit einer Wahrscheinlichkeit von 4/7), sind noch 6 Kugeln übrig: 3 rote und 3 schwarze. Das gibt zwei neue Verzweigungen: links rot mit einer Wahrscheinlichkeit von 3/6 und rechts schwarz mit einer Wahrscheinlichkeit von 3/6.
Die Wahrscheinlichkeit, dass auf diesem Weg durch den Baum zweimal schwarz gezogen wird, ist nach der Pfadmultiplikationsregel: 4/7 × 3/6 = 12/42 = 2/7 (ca. 28,6 %).
Addition der Wahrscheinlichkeiten
Nun werden die Wahrscheinlichkeiten für rot-rot und schwarz-schwarz nach der Pfadadditionsregel aufaddiert: 1/7 + 2/7 = 3/7.
Die Wahrscheinlichkeit, dass beide Kugeln dieselbe Farbe haben, ist 3/7 (circa 42,9 %).
Genauso lassen sich andere Wahrscheinlichkeiten entlang der Baumstruktur berechnen.