Höchstpreis
Definition
Bei staatlich festgelegten Höchstpreisen (Beispiel: Mietpreisbremse) wird im Vergleich zu dem üblichen (höheren) Gleichgewichtspreis mehr nachgefragt als angeboten, es kommt zu einem Nachfrageüberhang.
Beispiel
Die Wirkung eines Höchstpreises kann man anhand des Beispiels zum Gleichgewichtspreis sehen:
Ohne Höchstpreis
Hier noch mal wiederholt die Ausgangssituation vom Marktgleichgewicht:
Auf einem Wochenmarkt werden Hühnereier der Grösse M durch mehrere Anbieter verkauft.
Bei einem Preis pro Ei von 1 € werden 100 Stück angeboten und das Angebot nimmt jeweils um 10 Eier ab, wenn der Preis jeweils um 0,10 € sinkt (das heißt, bei 0,90 € werden nur 90 Eier angeboten, bei 0,80 € dann 80 Eier und so weiter).
Als Angebotsfunktion: ANGEBOTSMENGE = 100 × PREIS.
Bei der Nachfrage verhält es sich anders herum: Zu einem Preis von 1 € kaufen die Leute keine Eier, fällt der Preis jedoch jeweils um 0,10 €, steigt die Nachfrage um 10 Eier (das heißt, bei 0,90 € werden 10 Eier nachgefragt, bei 0,80 € dann 20 Eier und so weiter).
Als Nachfragefunktion: NACHFRAGEMENGE = 100 - 100 × PREIS.
Der Gleichgewichtspreis lässt sich berechnen, indem man die Angebotsfunktion der Nachfragefunktion gegenüberstellt und nach dem PREIS auflöst:
100 × PREIS = 100 - 100 × PREIS
200 × PREIS = 100
PREIS = 0,50 €.
Bei einem Preis von 0,50 € werden 50 Eier angeboten (Angebotsmenge = 100 × 0,50 = 50) und 50 Eier nachgefragt (Nachfragemenge = 100 - 100 × 0,50 = 50), die Gleichgewichtsmenge ist 50 Stück.
Der Umsatz auf dem Markt beträgt: 50 Eier × 0,50 € = 25 €.
Mit Höchstpreis
Würde man einen Höchstpreis für Hühnereier bei 0,40 € festlegen (0,10 € unter dem Gleichgewichtspreis von 0,50 €), würden nur 40 Eier angeboten, aber 60 Eier nachgefragt; 20 Eier würden fehlen.
Diesen Nachfrageüberhang in der Grafik dargestellt:
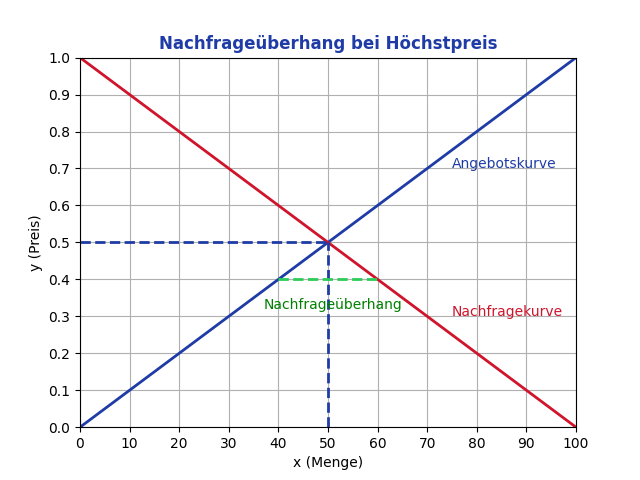
Der Marktumsatz wäre 40 Eier × 0,40 € = 16 € (viel weniger als beim Gleichgewichtspreis mit einem Marktumsatz von 50 Eier × 0,50 € = 25 €).