Hypergeometrische Verteilung
Hypergeometrische Verteilung Definition
Die hypergeometrische Verteilung kann anhand des Urnenmodells mittels Ziehen ohne Zurücklegen dargestellt werden:
Aus einer Urne mit Kugeln zweier Farben (zum Beispiel schwarz und weiß) werden eine bestimmte Anzahl von Kugeln ohne Zurücklegen (der gezogenen Kugeln) gezogen. Bekannt ist die Aufteilung der Kugeln auf die beiden Farben schwarz und weiß.
Frage
Beispielhafte Fragestellung: Wie hoch ist die Wahrscheinlichkeit, dass bei einer Ziehung von 3 Kugeln (Stichprobenumfang) aus einer Grundgesamtheit von 10 Kugeln (von denen 20 % schwarz und 80 % weiß sind) genau 1 Kugel schwarz ist?
Formel
Die Formel für die Hypergeometrische Verteilung ist:
$$H (x, n, N, M) = \frac{\binom{M}{x} \cdot \binom{N - M}{n - x}}{\binom{N}{n}}$$
Man benötigt also 3 Binomialkoeffizienten.
Dabei ist N die Menge (Anzahl), aus der gezogen wird; M die Teilmenge, die eine bestimmte Eigenschaft hat; n der Stichprobenumfang und x ist der Wert, für den die Wahrscheinlichkeit gesucht wird.
Beispiele
Beispiel 1: Hypergeometrische Verteilung
Bei der Inventur werden in einem Regallager 10 Motoren eines Typs gezählt. Aus Erfahrung weiß man, dass 20 % der Motoren defekt sind (das heißt, von den 10 Motoren sind 2 defekt und 8 in Ordnung). Der Inventurleiter entnimmt 3 Motoren und lässt diese überprüfen.
Wie hoch ist die Wahrscheinlichkeit, dass genau 1 Motor (aus der entnommenen Stichprobe von 3 Motoren) defekt ist?
Wahrscheinlichkeit
Die hypergeometrische Wahrscheinlichkeit ist:
$$H (1, 3, 10, 2) = \frac{\binom{2}{1} \cdot \binom{10 - 2}{3 - 1}}{\binom{10}{3}} = \frac{\binom{2}{1} \cdot \binom{8}{2}}{\binom{10}{3}}$$
$$= \frac{2 \cdot 28}{120} = \frac{56}{120} = 0,467$$
Die Wahrscheinlichkeit ist also circa 46,7 %.
Dabei ist 2 die Anzahl der defekten Motoren in der Grundgesamtheit, (10 - 2) die Anzahl der nicht defekten Motoren in der Grundgesamtheit, 10 ist die Grundgesamtheit, 3 ist der Stichprobenumfang und 1 ist die Anzahl der defekten Motoren in der Stichprobe, für die die Wahrscheinlichkeit gesucht wird.
Zur Erinnerung: Die Formel für den Binomialkoeffizienten B (n über k) bzw. B (k aus n) (mit ! als Zeichen für Fakultät) ist:
$$\binom{n}{k} = \frac{n!}{[ (n - k)! \times k ! ]}$$
Im Beispiel oben für den Nenner: (3 aus 10) = 10! / [ (10 - 3)! × 3! ] = 10! / (7! × 3!) = 120.
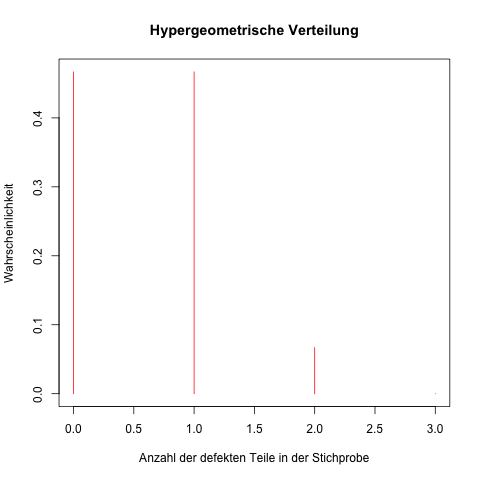
Graph
Als Grafik mit den gerundeten Wahrscheinlichkeiten für 0 (0,467), 1 (0,467) oder 2 (0,067) defekte Motoren in der Stichprobe (mehr defekte Motoren gibt es nicht):
Beispiel 2: Wahrscheinlichkeit für "3 Richtige"
Mit der hypergeometrischen Verteilung lässt sich die Wahrscheinlichkeit für "3 Richtige" im Lotto "6 aus 49" berechnen.
Dabei gibt es 49 Kugeln, von denen 6 "richtig" sind und 43 "falsch"; die Stichprobe umfasst 6 Ziehungen (ohne Zurücklegen).
"3 Richtige" bedeutet, dass man 3 aus den 6 richtigen und 3 aus den restlichen 43 falschen Kugeln zieht; die Wahrscheinlichkeit für 3 Richtige ist:
$$H (3, 6, 49, 6) = \frac{\binom{6}{3} \cdot \binom{43}{3}}{\binom{49}{6}} = \frac{20 \cdot 12.341}{13.983.816}$$
$$= 246.820 / 13.983.816 = 0,01765$$
Die Wahrscheinlichkeit ist circa 1,77 %.