Poisson-Verteilung
Poisson-Verteilung Definition
Die Poisson-Verteilung ist eine der diskreten Wahrscheinlichkeitsverteilungen.
Typische Fragestellungen, die sich mit Hilfe der Poisson-Verteilung beantworten lassen, sind die
- nach der Anzahl von Ereignissen innerhalb einer bestimmten Zeiteinheit (zum Beispiel Anzahl der eingehenden Telefonanrufe in einem Callcenter innerhalb einer Stunde oder Anzahl der Kunden in einem Supermarkt innerhalb einer Stunde) oder die
- nach der Anzahl von Objekten auf einer bestimmten Fläche (zum Beispiel Anzahl der Maulwurfshügel auf einem Hektar) oder in einem bestimmten Volumen (zum Beispiel Anzahl der Bakterien in einem Liter Flüssigkeit).
Die Poisson-Verteilung hat nur einen Parameter λ (Lambda), der die durchschnittliche bzw. erwartete Häufigkeit des Eintretens eines Ereignisses in einem Intervall beschreibt (zum Beispiel 5 Kundenbesuche pro Stunde) — kennt man diesen Parameter (und sind die weiter unten genannten Voraussetzungen erfüllt), hat man alles, um Wahrscheinlichkeiten zu berechnen.
Ist eine Variable poissonverteilt, schreibt man dies in der Regel so:
x ~ Poi (λ = 5) mit λ als einzigem Parameter.
Bei der Poisson-Verteilung sind der Erwartungswert und die Varianz gleich λ und damit identisch; die Standardabweichung ist $\sqrt{\lambda}$.
Die Poisson-Verteilung wird auch als Näherungslösung für die Binomialverteilung (sogenannte Poisson-Approximation) verwendet und zwar dann, wenn die Anzahl der Versuchsdurchführungen hoch ist (zum Beispiel ab 100) und die (Erfolgs-)wahrscheinlichkeit für das Eintreffen eines Ereignisses gering (zum Beispiel maximal 10 %). Sie wird auch als Verteilung der seltenen Ereignisse bezeichnet und für die Wahrscheinlichkeitsberechnung von Unfällen, Maschinenausfällen und so weiter verwendet.
Beispiel
Poissonverteilung Beispiel
Im Durchschnitt kommen in ein Fachgeschäft unabhängig von der Tageszeit 5 Kunden pro Stunde.
Wie hoch ist die Wahrscheinlichkeit, dass kein Kunde innerhalb eines Ein-Stunden-Zeitraums den Laden betritt?
Formel für Wahrscheinlichkeitsfunktion
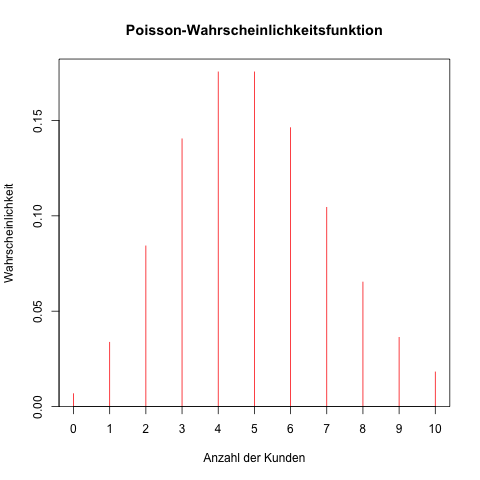
Die Wahrscheinlichkeitsfunktion gibt an, mit welcher Wahrscheinlichkeit genau eine bestimmte Anzahl von Ereignissen eintritt (genau 0 Kundenbesuche, genau 1 Kundenbesuch und so weiter).
Die Formel für die Wahrscheinlichkeitsfunktion der Poisson-Verteilung ist:
$$P(x) = \frac{λ^x \cdot e^- λ}{x!}$$
mit
- x = Anzahl der Ereignisse in einem bestimmten Zeitraum (hier: 0 Kundenbesuche innerhalb einer Stunde)
- P(x) = Wahrscheinlichkeit, dass x Ereignisse innerhalb des Zeitraums eintreten
- x! = x Fakultät (zum Beispiel 3! = 3 × 2 × 1 = 6), für den Fall x = 0 wird die Fakultät mit 1 definiert
- λ (Lamda) gleich dem Erwartungswert bzw. Durchschnittswert, Lamda ist hier 5 (Kundenbesuche)
- e gleich der Eulerschen Zahl: 2,71828 (wenn man sie mit nur 5 Nachkommastellen darstellt).
Berechnung
P (0) = (5 0 × e -5) / 0! = e -5 = 0,006738.
Das heißt, die Wahrscheinlichkeit dafür, dass kein Kunde innerhalb von einer Stunde den Laden betritt, ist mit 0,006738 bzw. gerundet 0,67 % sehr gering.
Die Wahrscheinlichkeitsfunktion für die Poisson-Verteilung mit λ = 5 und für 0 bis 10 Kunden pro Stunde gezeichnet ist:
Formel für Verteilungsfunktion
Die Verteilungsfunktion gibt an, mit welcher Wahrscheinlichkeit maximal eine bestimmte Anzahl von Ereignissen eintritt (maximal 0 Kundenbesuche, maximal 1 Kundenbesuch und so weiter).
Dafür müssen die einzelnen Wahrscheinlichkeiten hier kumuliert werden.
Die Formel für die Verteilungsfunktion der Poisson-Verteilung ist:
$$P(X \le x) = \sum_{k= 0}^x P(k)$$
Fragestellung: Wie hoch ist die Wahrscheinlichkeit, dass weniger als 2 Kunden (also maximal 1 Kunde) innerhalb eines Ein-Stunden-Zeitraums den Laden betreten?
In dem Fall setzt sich die Lösung aus P(0) + P(1) zusammen.
P (1) = (5 1 × e -5) / 1! = (5 × e -5) / 1 = 0,03369.
Die Wahrscheinlichkeit, dass 1 Kunde den Laden betritt, ist 0,03369 bzw. gerundet 3,37 %.
Damit ist P(x <= 1) = 0,67 % + 3,37 % = 4,04 %.
Die Verteilungsfunktion für die Poisson-Verteilung mit λ = 5 und für maximal 10 Kunden pro Stunde gezeichnet ist:
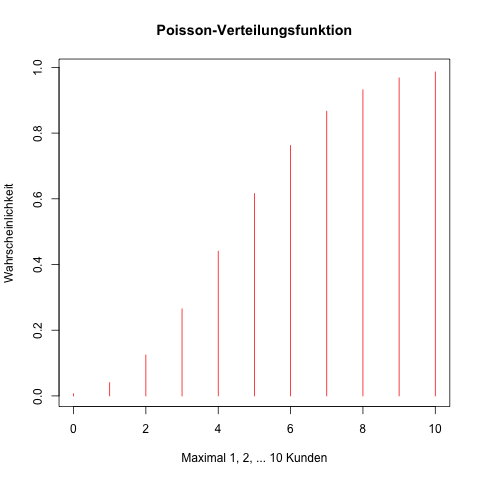
Die Wahrscheinlichkeit, dass in einer Stunde maximal 10 Kunden den Laden betreten ist circa 98,6 %.
Kann eine Verkäuferin allein zum Beispiel maximal 10 Kunden pro Stunde bewältigen, kann der Geschäftsinhaber ziemlich sicher (98,6 %) sein, dass es keine Probleme geben wird.
Voraussetzungen und Anwendung
Voraussetzung der Poisson-Verteilung ist, dass
- es sich um eine diskrete Zufallsvariable handelt,
- die Ereignisse zufällig sind (und nicht zum Beispiel einer Planung wie einem Stunden- oder Fahrplan folgend auftreten) und
- die Ereignisse unabhängig voneinander sind (das Eintreten bzw. Nichteintreten eines Ereignisse beeinflusst nicht das folgende Eintreten bzw. Nichteintreten eines weiteren Ereignisses).
Manchmal passen die vorhandenen Daten nicht zur Fragestellung.
Beispiel: In einem Unternehmen werden statistisch die Arbeitsunfälle je 100.000 Arbeitsstunden erfasst, sagen wir: 2,5. Möchte man nun beispielsweise die Wahrscheinlichkeit berechnen, dass in den nächsten 40.000 Arbeitsstunden kein Unfall passiert, muss man umrechnen: (40.000/100.000) × 2.5 = 1. Mit diesem λ von 1 wird dann weitergerechnet.
Poisson-Approximation
Wenn die Anzahl der Durchführungen des Experiments hoch ist und die Wahrscheinlichkeit gering, kann die Binomialverteilung durch die Poisson-Approximation angenähert werden.
Beispiel: Poisson-Approximation
Das obige Experiment soll wie folgt modelliert werden: Die Wahrscheinlichkeit, dass ein Kunde in einem Zeitintervall von 1 Sekunde den Laden betritt, ist 5/3.600 (5 Besucher pro Stunde, eine Stunde hat 3.600 Sekunden), die Gegenwahrscheinlichkeit ist dann 3.595/3.600.
Damit hat man eine hohe Anzahl von Durchführungen (3.600) und eine sehr geringe (Erfolgs)wahrscheinlichkeit.
Die Wahrscheinlichkeit für 0 Besuche nach der Formel für die Binomialverteilung ist:
P (0) = { 3.600! / [ 0! × (3.600 - 0)! ] } × 5/3.600 0 × (3.595/3.600) (3.600 -0)
= 1 × 1 × (3.595/3.600) (3.600) = 0,00671 (auf 5 Stellen gerundet) = 0,67 % (annähernd wie oben)
Analog für die Wahrscheinlichkeit eines Besuchs:
P (1) = { 3.600! / [ 1! × (3.600 - 1)! ] } × 5/3.600 1 × (3.595/3.600) (3.600 -1)
= 3.600 × (5/3.600) 1 × (3.595/3.600) 3.599 = 0,03362 (auf 5 Stellen gerundet) = 3,36 % (annähernd wie oben)
Im Beispiel wird bereits mit hohen Fakultäten und Exponenten gerechnet, die Poisson-Verteilung ist rechentechnisch einfacher.