Trapezregel

Beispiel Trapezregel

Die Funktion sei y = x².

Die Fläche unter der Funktionskurve im Bereich von x = 1 bis x = 3 soll durch ein Trapez angenähert werden.

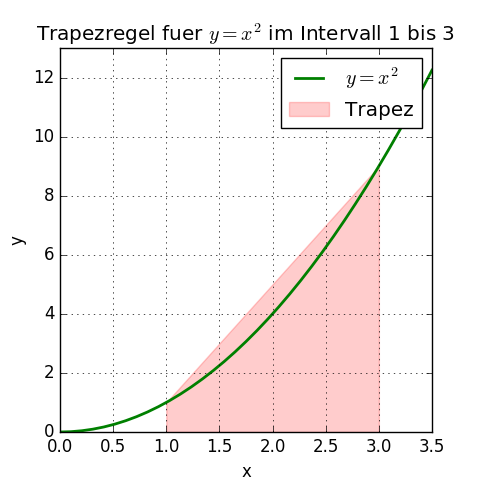
Man sieht in der Grafik, dass die Fläche des Trapezes etwas größer ist als die Fläche unter der Kurve – es ist nur eine Näherung, die durch mehr Trapeze verfeinert werden kann.

Die Fläche eines Trapezes ist: $\frac{1}{2} \cdot h \cdot (a + b)$.

Dabei ist die Höhe h hier 2 (die Strecke im Intervall von 1 bis 3), a ist die linke Trapezseite mit einem Wert von f(1) = 1² = 1 und b ist die rechte Trapezseite mit einem Wert von f(3) = 3² = 9.

Fläche = $\frac{1}{2} \cdot 2 \cdot (1 + 9) = 10$

Die Näherung kann durch mehr Trapeze verbessert werden, da sich diese näher an die Kurve anschmiegen.

Zum Beispiel bei 2 Trapezen:

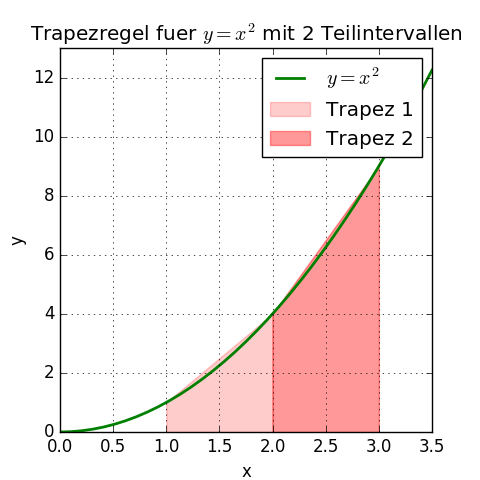
Trapez 1 hat die Fläche $\frac{1}{2} \cdot 1 \cdot (f(1) + f(2)) = \frac{1}{2} \cdot (1 + 4) = 2.5$

Trapez 2 hat die Fläche $\frac{1}{2} \cdot 1 \cdot (f(2) + f(3)) = \frac{1}{2} \cdot (4 + 9) = 6.5$

Hinweis: die Höhe der Trapeze ist nunmehr nur noch 1 (bei 4 Trapezen wäre die Höhe dann 0,5 und so weiter).

Addiert man die beiden Trapeze auf, ergibt sich die näherungsweise Fläche: 2,5 + 6,5 = 9.

Kontrolle (mit Integral)

Wir prüfen mit einer genauen Integralberechnung, ob dies eine gute Näherung ist.

Dafür suchen wir zunächst eine Stammfunktion F(x), das heißt eine Funktion, die abgeleitet die Funktion f(x) = x² ergibt, zum Beispiel $F(x) = \frac{1}{3} x^3$.

Anschließend berechnen wir das Integral (siehe Bestimmtes-Integral):

$$\int_1^3 f(x) dx$$

$$= \left[\frac{1}{3} x^3 \right]_1^3$$

$$= \frac{1}{3} \cdot 3^3 - \frac{1}{3} \cdot 1^3 = 9 - \frac{1}{3} = 8 \frac{2}{3}$$

Die tatsächliche Fläche mit einem Integral berechnet ist also gerundet 8,67.

Die Abweichung der Näherung ist hier mit 1/3 bereits unter 5 % und kann durch weitere Unterteilung in beispielsweise 4 oder 8 Intervalle / Trapeze noch verbessert werden.