Berührpunkt
Berührpunkt Definition
Möchte man wissen, ob sich zwei Funktionen / Graphen / Kurven in einem (zu findenden) Punkt x0 berühren, sind 2 Voraussetzungen zu prüfen:
- Sind die Funktionswerte der beiden Funktionen bei x0 gleich? Das wäre allerdings auch bei Schnittpunkten so; deshalb gibt es eine zweite Bedingung:
- Sind die Tangentensteigungen (die 1. Ableitungen der beiden Funktionen) in dem Punkt x0 gleich?
Bedingungen
Im Berührpunkt x0 gilt also für 2 Funktionen f(x) und g(x):
f(x0) = g(x0) (Funktionswerte gleich)
f’(x0) = g’(x0) (Erste Ableitungen gleich)
Beispiel
Beispiel: Berührpunkt berechnen
Die Funktionen seien $f(x) = x^2 + 1$ und $g(x) = -(x^2) + 1$
Grafisch
In der Grafik sieht man schon, dass bei dem Punkt (0 | 1) ein Berührpunkt ist:
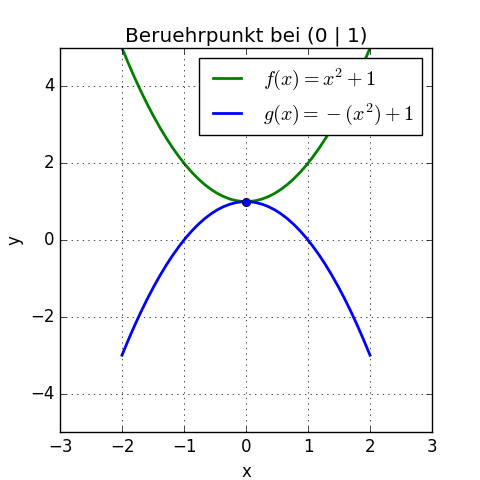
Rechnerisch
Die beiden Funktionen gleichsetzen:
$$f(x) = g(x)$$
$$x^2 + 1 = -(x^2) + 1$$
$$x^2 = -(x^2)$$
Das ist nur für x = 0 der Fall:
$$0^2 = -(0^2)$$
Das kann ein Berührpunkt oder ein Schnittpunkt sein.
Zweite Bedingung für Berührpunkt prüfen: Tangentensteigung identisch?
Dazu werden die ersten Ableitungen der beiden Funktionen gebildet und an der Stelle x0 = 0 gleichgesetzt:
$$f'(x) = 2x$$
$$g'(x) = -(2x)$$
Gleichsetzung:
$$f'(x_0) = g'(x_0)$$
$$2 \cdot 0 = - (2 \cdot 0)$$
$$0 = 0$$
Da die beiden Seiten gleich sind und damit die zweite Bedingung (gleiche Tangentensteigung) erfüllt ist, liegt ein Berührpunkt vor (würde hier zum Beispiel 1 = 3 stehen, läge kein Berührpunkt vor).
y-Koordinate des Berührpunkts: $f(0) = 0^2 + 1 = 1$ oder $g(0) = -(0^2) + 1 = 1$
Ergebnis
Der Berührpunkt liegt also bei der x-Koordinate 0 und der y-Koordinate 1; kurz: beim Punkt (0 | 1).
Für x = 0 sind die Funktionswerte und die ersten Ableitungen der beiden Funktionen identisch.