Fläche zwischen zwei Graphen

Fläche zwischen zwei Graphen Definition

Die Fläche zwischen zwei Graphen / Funktionen / Kurven in einem Intervall kann mit einem Integral berechnet werden.

Beispiel

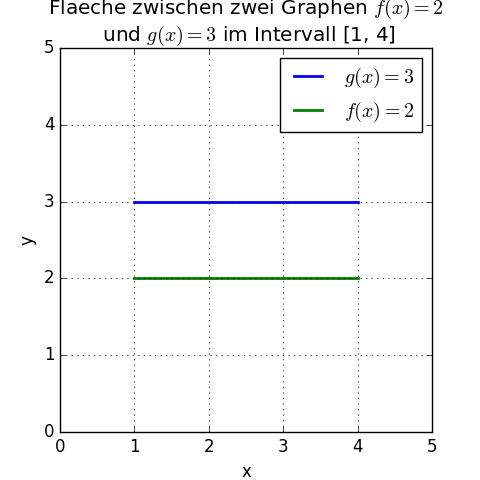
Wir nehmen hier zwei sehr einfache Graphen, nämlich zwei konstante Funktionen im Intervall von 1 bis 4:

f(x) = 2

g(x) = 3

Die Fläche zwischen der "oberen Funktion" g(x) – die im Intervall immer oberhalb der anderen Funktion liegt – und der "unteren Funktion" f(x) im Intervall [1, 4] ist 3 cm², wie man leicht sehen kann (die Fläche zwischen den beiden Linien):

Die Fläche mit dem Integral berechnet ist:

$$\int_1^4 [g(x) - f(x)] \, dx$$

Das lässt sich über die Stammfunktionen berechnen. Eine Stammfunktion F(x) für f(x) – d.h. eine Funktion, die abgeleitet f(x) ergibt – wäre z.B. F(x) = 2x, eine Stammfunktion G(x) für g(x) wäre z.B. G(x) = 3x.

Integral berechnen:

$$\int_1^4 [g(x) - f(x)] \,dx$$

$$= \left[3x - 2x \right]_1^4$$

$$= (3 \cdot 4 - 2 \cdot 4) - (3 \cdot 1 - 2 \cdot 1)$$

$$=(12 - 8) - (3 - 2) = 4 - 1 = 3$$

Alternative Begriffe: Fläche zwischen zwei Funktionen, Fläche zwischen zwei Funktionsgraphen, Fläche zwischen zwei Kurven, Flächeninhalt zwischen zwei Graphen, Integral zwischen zwei Funktionen.