Flächenbilanz
Definition
Bei einem Integral kann der Integrand (die zu integrierende Funktion) je nach Funktion auch negative Funktionswerte annehmen.
Dann spiegelt die Integralfunktion eine sogenannte Flächenbilanz wider, bei der von den positiven Flächen oberhalb der waagrechten x-Achse die negativen Flächen unterhalb der x-Achse abgezogen werden.
Man kann sich die zweidimensionale Aufnahme eines Eisbergs vorstellen: von der Fläche oberhalb der Wasseroberfläche wird die – in der Regel größere – Fläche unterhalb der Wasseroberfläche abgezogen, die Flächenbilanz wäre dann negativ.
Würde man hingegen den Flächeninhalt berechnen, würde man beide Flächen addieren.
Beispiel
Die zu integrierende Funktion sei $f(x) = \frac{1}{2}x - 1$.
Soll die Flächenbilanz im Intervall [0, 6] berechnet werden, kann man die Funktion in ein Koordinatensystem einzeichnen.
Flächenbilanz berechnen
Optisch
Im Intervallbereich 0 bis 2 ist der Funktionsgraph im negativen Bereich unterhalb der x-Achse (bei x = 2 ist der Funktionswert = 0), man kann die Flächeneinheiten (Kästchen) zwischen Funktionsgraph und x-Achse auszählen, in Summe ist die "negative Fläche" 1 cm2.
Im Intervallbereich 2 bis 4 ist der Funktionsgraph im positiven Bereich oberhalb der x-Achse, man kann die Flächeneinheiten (Kästchen) auszählen, in Summe sind es 4 cm2.
Die Flächenbilanz ist 4 cm2 - 1 cm2 = 3 cm2.
Mit Integral
Dasselbe Ergebnis erhält man auch, wenn man das bestimmte Integral berechnet:
$$\int_0^6 (\frac{1}{2}x - 1) \, dx$$
Eine Stammfunktion F(x) suchen, das heißt eine Funktion, die abgeleitet die Funktion ergibt, zum Beispiel:
$$F(x) = \frac{1}{4} x^2 - x$$
Integral berechnen:
$$\int_0^6 f(x) dx$$
$$= \left[\frac{1}{4} x^2 - x \right]_0^6$$
$$= (\frac{1}{4} \cdot 6^2 - 6) - (\frac{1}{4} \cdot 0^2 - 0)$$
$$= \frac{1}{4} \cdot 36 - 6 = 9 - 6 = 3$$
Grafik
Die Flächenbilanz graphisch:
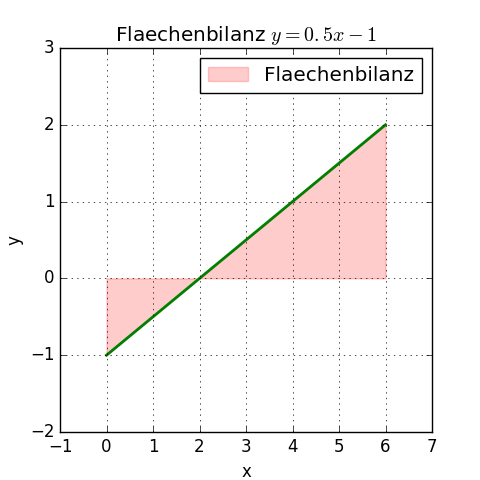
Das linke Dreieck unter der x-Achse hat eine negative Fläche von 0,5 × 2 cm × 1 cm = 1 cm2.
Das rechte Dreieck oberhalb der x-Achse hat eine positive Fläche von 0,5 × 4 cm × 2 cm = 4 cm2.
Die Differenz (die Flächenbilanz) ist 3 cm2.