Ertragsgesetzliche Produktionsfunktion
Definition
Die Ertragsgesetzliche Produktionsfunktion bzw. das Ertragsgesetz besagen:
Steigert man den Einsatz eines Produktionsfaktors (zum Beispiel Arbeit), erhöht sich der Output zunächst überproportional, später (mit zunehmender Arbeit) dann unterproportional, das heißt, der Grenzertrag sinkt.
Diese Gesetzmäßigkeit wurde ursprünglich für die Landwirtschaft entdeckt: durch Einsatz von Düngemitteln konnte der Ertrag – bei konstanter Anbaufläche – zunächst überproportional gesteigert werden, weitere Erhöhungen des Düngemitteleinsatzes brachten dann immer weniger.
Das dürfte vielleicht auch für Werbemaßnahmen gelten: durch mehr Werbung kann zunächst der Umsatz gegebenenfalls stark gesteigert werden, weitere Werbemaßnahmen bringen dann wahrscheinlich immer weniger.
Alternative Begriffe: Produktionsfunktion Typ A.
Bildliche Vorstellung
Trägt man in einem Koordinatensystem auf der waagrechten x-Achse die Düngemittelmenge (Produktionsfaktor) ab und auf der senkrechten y-Achse den Ernteertrag (Output), kann man sich die ertragsgesetzliche Produktionsfunktion graphisch als Umriß eines Hügels vorstellen:
Zunächst steigen die Erträge mit zunehmendem Düngemitteleinsatz steil an (hohe Ertragszuwächse), der Grenzertrag nimmt zu (was man über die 1. Ableitung der Produktionsfunktion sehen kann).
Dann geht es weniger steil weiter (geringere Ertragszuwächse, der Grenzertrag nimmt ab) bis zum höchsten Punkt des Hügels; anschließend fallen die Erträge sogar ab (Überdüngung, Boden beschädigt).
Schematisch als Grafik:
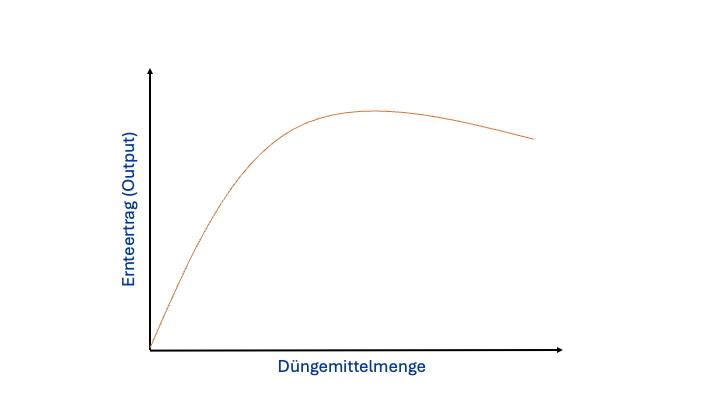
Dieser Zusammenhang gilt nach der Theorie (in der Landwirtschaft), wenn nur ein Produktionsfaktor (hier: Dünger) erhöht wird, und die anderen Produktionsfaktoren (etwa die Anbaufläche) konstant bleiben.
Mit mehr Anbaufläche und mehr Dünger (also Erhöhung mehrerer bzw. aller Produktionsfaktoren) kann der Ertrag natürlich gesteigert werden.
Anwendung
Auf industrielle Produktionsprozesse in der Praxis ist das nur begrenzt übertragbar – das "Gesetz" gilt also nicht zwingend für alle (Produktionen).