Leontief-Produktionsfunktion
Leontief-Produktionsfunktion Definition
Bei der Leontief-Produktionsfunktion müssen die Einsatzfaktoren in einem konstanten Verhältnis genutzt werden. Wenn der Output erhöht werden soll, müssen die Einsatzfaktoren proportional erhöht werden. Das ist meistens so:
Beispiel
Ein Auto benötigt 4 Reifen und 5 Minuten Montagezeit für die Reifen. Sollen 2 Autos gebaut werden, benötigt man 8 Reifen und 10 Minuten Arbeitszeit.
Es werden modellhaft immer nur 2 Einsatzfaktoren betrachtet; ein Auto hat natürlich hunderte Einsatzfaktoren (die auch in demselben fixen Verhältnis erhöht werden müssen: 1 Lenkrad mehr, 1 Motor mehr etc.), man könnte diese in 2 Gruppen aufteilen: Material und Arbeit.
Die Leontief-Produktionsfunktion als Formel:
$$y = f(x_1, x_2) = min \{ \frac{x_1}{a}, \frac{x_2}{b}\} $$
Dabei sind x1 und x2 die Inputfaktoren, y ist der Output und a und b sind Produktionskoeffizienten.
Für das Autobeispiel
Die (konstanten) Produktionskoeffizienten sind: a = 4 und b = 5. Angenommen, man hat 8 Reifen und 15 Minuten verfügbare Arbeitszeit.
y = f(8, 15) = min {8/4, 15/5} = min {2, 3} = 2.
Es lassen sich also 2 Autos bauen und ein Teil der Arbeitszeit wird nicht genutzt.
Es handelt sich um eine limitationale Produktionsfunktion: ein Faktor beschränkt den Output, es ist keine Substitution möglich (kein Ersatz des einen Faktors durch den anderen).
Die entsprechenden Isoquanten sind L-förmig:
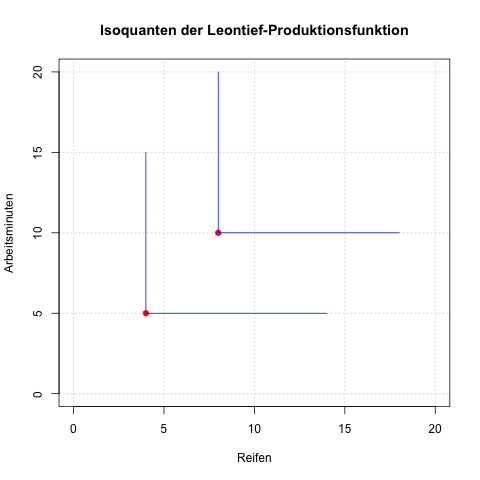
Die roten Punkte bei den Koordinaten (4,5) und (8,10) stellen die Faktorkombinationen dar, mit denen ein bzw. zwei Autos produziert werden können, ohne dass Einsatzfaktoren "übrig bleiben" (man sagt, diese sind effiziente Faktorkombinationen). Hätte man 4 Reifen und 6 Minuten oder 7 Minuten oder ..., bliebe es bei einem Auto; das spiegelt die Isoquante wider.
Die Substitutionselastizität der Leontief-Produktionsfunktion ist 0.