Integralfunktion
Integralfunktion Definition
Eine Integralfunktion ist eine Funktion, die – geometrisch betrachtet – in Abhängigkeit von einer Variablen x den Flächeninhalt zwischen Funktionsgraph und waagrechter x-Achse im Bereich zwischen einem vorgegebenen Startpunkt auf der x-Achse (z.B. 1) bis zum variablen Endpunkt x auf der x-Achse angibt.
Das ist analog dem bestimmten Integral, nur dass die obere Grenze nicht auch wie die untere Grenze fest, sondern variabel ist.
Beispiel
Eine Funktion sei f(t) = t.
Dazu soll folgende Integralfunktion gebildet werden:
$$F(x) = \int_1^x t \, dt$$
Der Funktionswert hängt also von x – der oberen Grenze – ab.
Nun wird eine Stammfunktion von f(t) berechnet (d.h. eine Funktion, die abgeleitet f(t) ergibt): F(t) = $\frac{1}{2} t^2$ (leitet man diese Funktion ab, erhält man t). Anschließend setzt man die obere Grenze x und die untere Grenze 1 ein.
$$\int_1^x t \, dt = \left[\frac{1}{2} t^2 \right]_1^x = \frac{1}{2} \cdot x^2 - \frac{1}{2} \cdot 1^2$$
$$= \frac{1}{2} \cdot x^2 - \frac{1}{2}$$
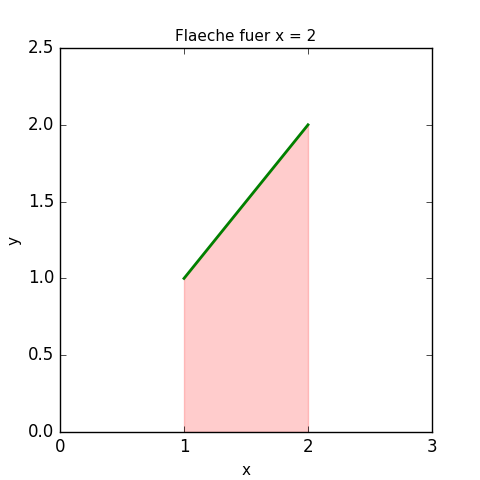
Für x = 2 ist die Fläche $F(2) = \frac{1}{2} \cdot 2^2 - \frac{1}{2} = \frac{3}{2} = 1,5$ (das entspricht der Fläche unter dem Funktionsgraphen im Intervall 1 bis 2: eineinhalb "Kästchen" mit einer Kantenlänge von 1 cm bzw. in Summe 1,5 cm2).
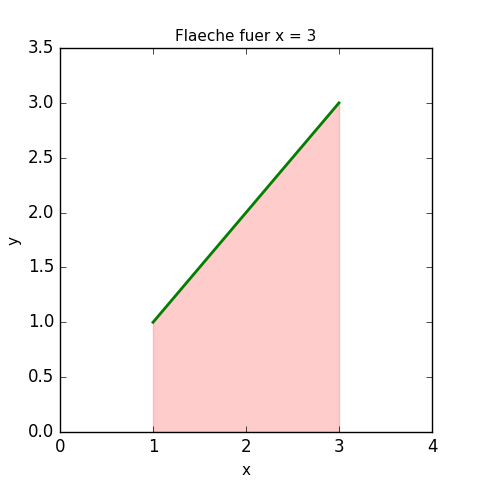
Für x = 3 ist die Fläche $F(3) = \frac{1}{2} \cdot 3^2 - \frac{1}{2} = \frac{8}{2} = 4$ (das entspricht der Fläche unter dem Funktionsgraphen im Intervall 1 bis 3).
usw.
Integralfunktion zeichnen
Die Integralfunktion kann man zeichnen:
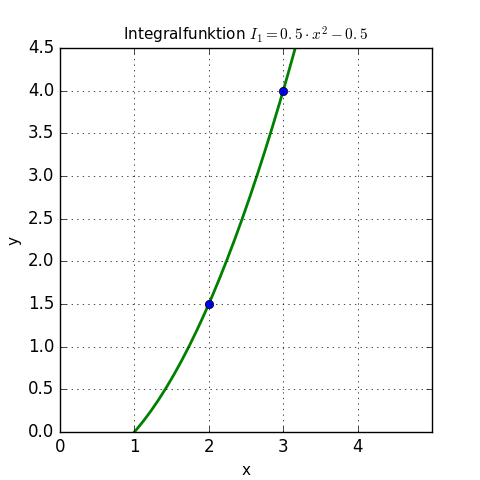
Die Flächenwerte lassen sich ablesen (die beiden eingezeichneten Punkte entsprechen den beiden Beispielwerten oben: eine Fläche von 1,5 für x = 2 und eine Fläche von 4 für x = 3).
Bei x = 1 (d.h. x gleich der unteren Integrationsgrenze) hat die Integralfunktion auf jeden Fall eine Nullstelle (daneben kann sie noch weitere Nullstellen haben).
Eine Integralfunktion ist also praktisch: man kann für verschiedene Grenzen schnell Integrale bzw. Flächen berechnen. Und man kann wie bei anderen Funktionen auch Nullstellen bestimmen, die Integralfunktion ableiten u.v.m.