Isoquante
Definition
Eine Isoquante stellt alle Kombinationen von Produktionsfaktoren (Input) dar, die ein und dieselbe (festgelegte) Ausbringungsmenge (Output) erzeugen.
Der Begriff leitet sich ab von iso = gleich (griechisch) und Quantum = Menge, also: gleiche Menge (an Output).
Üblicherweise bildet man ein Modell mit nur 2 Inputfaktoren, die substituierbar sind, also gegeneinander ausgetauscht werden können.
Um die Isoquante darstellen zu können, benötigt man eine Produktionsfunktion sowie die (gewünschte) Ausbringungsmenge.
Beispiel
Der Rasen eines großen Fußballstadions muss an einem Tag gemäht werden (Output hier: 8.000 qm gemähte Fläche). Zur Verfügung stehen
- Arbeiter mit einer Sichel, die 100 qm je Stunde mähen und je geleistete Arbeitsstunde bezahlt werden (Produktionsfaktor Arbeit) und
- Rasenmäh-Roboter, die 200 qm je Stunde schaffen und zu einer Mietgebühr je Stunde ausgeliehen werden können (Produktionsfaktor Kapital).
Der Output von 8.000 gemähten qm kann durch mehrere Kombinationen von Produktionsfaktoren erreicht werden, zum Beispiel:
- 10 Arbeiter mähen jeweils 8 Arbeitsstunden (80 Std. × 100 qm/Std. = 8.000 qm)
- 8 Arbeiter mähen 8 Stunden (64 Std. × 100 qm/Std. = 6.400 qm) und 1 Rasenmäh-Roboter mäht 8 Std. (8 Std. × 200 qm/Std. = 1.600 qm)
- ...
- 5 Rasenmäh-Roboter mähen jeweils 8 Std. (40 Std. × 200 qm/Std. = 8.000 qm).
Isoquanten können für verschiedene Outputniveaus gebildet und dargestellt werden (zum Beispiel für 8.000 qm wie im Beispiel, für 9.000 qm und für 10.000 qm), man erhält dann eine sogenannte Isoquantenschar.
Isoquante zeichnen
Der eine Produktionsfaktor wird auf der x-Achse, der zweite Produktionsfaktor auf der y-Achse abgetragen und die Isoquante ist dann die Kurve, die die eingezeichneten Punkte (Faktorkombinationen) verbindet.
Die Isoquante für den Output von 8.000 qm sieht so aus:
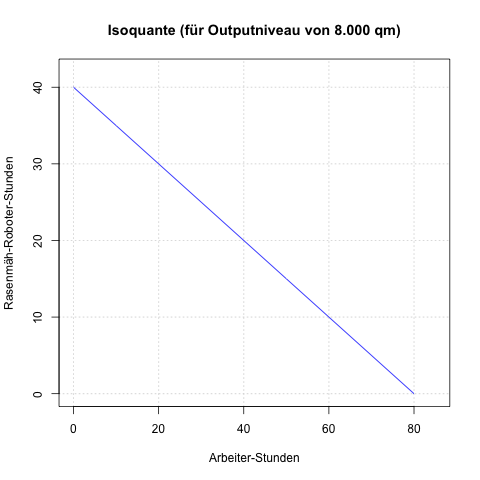
Es handelt sich hierbei um eine lineare Produktionsfunktion der Form:
y = 100 A + 200 R
Dabei ist y der Output (die gemähte Rasenfläche), A ist die Anzahl der Arbeitsstunden und R die Anzahl der Roboterstunden. Arbeiter- und Roboterstunden stellen hier perfekte Substitute dar, die gegeneinander in einem festen Verhältnis ausgetauscht werden können.
Isoquante berechnen
Um die Isoquante für einen Output von 8.000 qm zu zeichnen, kann man die Funktion nach dem zweiten Faktor R auflösen:
8.000 = 100 A + 200 R
8.000 - 100 A = 200 R
40 - 0,5 A = R
R auf der linken Seite darstellen:
R = 40 - 0,5 A
Dabei ist 40 der y-Achsenabschnitt und -0,5 ist die (negative) Steigung der Geraden (eine Einheit wie cm oder Kästchen nach rechts, eine halbe Einheit nach unten).
Die Grenzrate der technischen Substitution ist konstant und entspricht der Steigung der Geraden.
Typische Isoquanten
Zwei weitere typische Isoquanten sind:
Konstant proportional
Die beiden Inputfaktoren müssen in konstantem Verhältnis eingesetzt werden.
Beispiel
Einsatzfaktor 1 (Arbeiter, x1) und Einsatzfaktor 2 (elektrischer Rasenmäher, x2).
Ein weiterer Arbeiter ohne Rasenmäher bringt nicht mehr Output (gemähte Rasenfläche), ebensowenig wie ein weiterer Rasenmäher ohne Arbeiter, der ihn bedient.
Nur in konstantem Verhältnis erhöht (zum Beispiel 1 Arbeiter mehr und 1 Rasenmäher mehr) bringen sie mehr Output.
Als Funktion: f(x1, x2) = min {x1, x2}
Der kleinste Einsatzfaktor bestimmt bzw. limitiert den Output.
Perfekt substitutional mit 1-zu-1-Verhältnis
Die beiden Inputfaktoren lassen sich eins zu eins austauschen.
Beispiel
Einsatzfaktor 1 (Arbeiter mit Rasenmäher, x1) und Einsatzfaktor 2 (Rasenmäh-Roboter, x2) und beide schaffen je Stunde dieselbe gemähte Fläche.
Man kann Arbeiterstunden gegen Roboterstunden austauschen und umgekehrt, der Output bleibt konstant.
Als Funktion: f(x1, x2) = x1 + x2
Die Summe der Einsatzfaktoren bestimmt den Output.