Grenzrate der technischen Substitution
Definition
Die Grenzrate der technischen Substitution (GRTS) zweier modellhaft betrachteter Produktionsfaktoren gibt an, um wieviele Einheiten der Produktionsfaktor 2 erhöht werden muss (bzw. gesenkt werden kann), wenn – bei gleichem Output (Produktionsmenge) – der Produktionsfaktor 1 um eine Einheit reduziert (bzw. erhöht) wird.
Die GRTS entspricht der Steigung der Isoquante in einem bestimmten Punkt.
Alternativ wird für die GRTS auch der englische Begriff Marginal Rate of Technical Substitution (MRTS) verwendet.
Alternative Begriffe: Technische Rate der Substitution (TRS).
Beispiel
Wir greifen das Beispiel zur Isoquante auf:
Der Rasen eines großen Fußballstadions mit 8.000 qm Fläche muss an einem Tag gemäht werden (das ist der Output). Zur Verfügung stehen
- Arbeiter, die mit einem elektrischen Rasenmäher 100 qm je Stunde mähen und pro Arbeitsstunde bezahlt werden (Produktionsfaktor Arbeit) und
- Rasenmäh-Roboter, die 200 qm je Stunde mähen und zu einer Mietgebühr je Stunde ausgeliehen werden können (Produktionsfaktor Kapital).
Mähen 10 Arbeiter jeweils 8 Arbeitsstunden, schaffen sie so mit 80 Std. × 100 qm/Std. die gesamte Fläche von 8.000 qm.
Wird nun der Einsatz der Arbeiter um eine Einheit (1 Stunde) reduziert, muss der Rasenmähroboter 1/2 Stunde eingesetzt werden (0,5 Std. × 200 qm/Std. = 100 qm).
In der Grafik zur Isoquante sieht man es besser, wenn man sich vorstellt, dass die Arbeiterstunden um 20 zum Beispiel von 60 auf 40 reduziert werden; der Rasenmähroboter muss dann 10 Stunden mehr arbeiten, das heißt, von 10 auf 20 Stunden erhöhen:
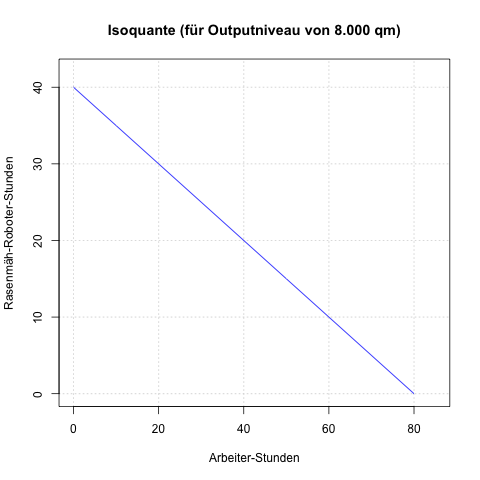
GRTS berechnen
Im obigen Beispiel kann man die GRTS bzw. das Austauschverhältnis zwischen Arbeiter- und Roboterstunden einfach erkennen bzw. in der Grafik ablesen.
In der Regel muss sie aber formal berechnet werden.
Dazu braucht man die Produktionsfunktion, um damit die Grenzprodukte der Produktionsfaktoren zu berechnen.
Es handelt sich hier um eine lineare Produktionsfunktion der Form y = 100 A + 200 R (mit y für Output, A für Arbeiterstunden und R für Roboterstunden).
Formel
GRTS = - (Grenzprodukt 1 / Grenzprodukt 2)
Grenzprodukt 1 wird mathematisch über die partielle Ableitung der Produktionsfunktion nach dem ersten Produktionsfaktor A abgebildet:
fA (A, B) = 100 (Ableitung einer Variablen A mit Faktor 100)
Bei einer Erhöhung des Inputfaktors A (und B bleibt konstant) erhöht sich der Output um 100 qm.
Analog für den zweiten Produktionsfaktor B:
fB (A, B) = 200 (Ableitung einer Variablen B mit Faktor 200)
Bei einer Erhöhung des Inputfaktors B (und A bleibt konstant) erhöht sich der Output um 200 qm.
Die Grenzrate der technischen Substitution ist dann: - (100 / 200) = - 0,5.
Das ist die (negative) Steigung der obigen Isoquante.
Interpretation
Da es sich um eine lineare Produktionsfunktion handelt, ist die GRTS konstant. Man kann also Arbeiter und Roboter immer im gleichen Verhältnis austauschen.
Oft ist die GRTS aber nicht konstant und es liegt eine abnehmende GRTS vor (die Isoquante ist nicht gerade, sondern kurvig).