Logarithmische Skala
Logarithmische Skala
Die meisten Skalen sind lineare Skalen, zum Beispiel ein Meterstab: die Zahlen auf der Skala nehmen mit gleichen Abständen um denselben Betrag zu: zwischen 1 cm und 2 cm ist derselbe Abstand wie zwischen 2 cm und 3 cm.
Bei einer logarithmischen Skala (zum Beispiel basierend auf Zehnerlogarithmen) ist das anders: hier ist "ein Abstand weiter" ein Veränderung um einen konstanten Faktor, zum Beispiel Verzehnfachung: 1, 10, 100, 1.000, 10.000.
Dabei ist 1 = 100, 10 = 101, 100 = 102, 1.000 = 103, 10.000 = 104 und so weiter, der Exponent nimmt jeweils um 1 zu.
Logarithmische Skalen werden unter anderem bei der Darstellung von Aktienkursverläufen eingesetzt.
Alternative Begriffe: Halblogarithmische Skala, Log-Skala, logarithmische Darstellung, logarithmische Skalierung, Logarithmus-Skala.
Beispiel
Beispiel: Lineare vs. logarithmische Skala
Ein Aktienkurs steigt in der ersten Woche von 8 € auf 16 €, in der zweiten Woche von 16 € auf 24 €.
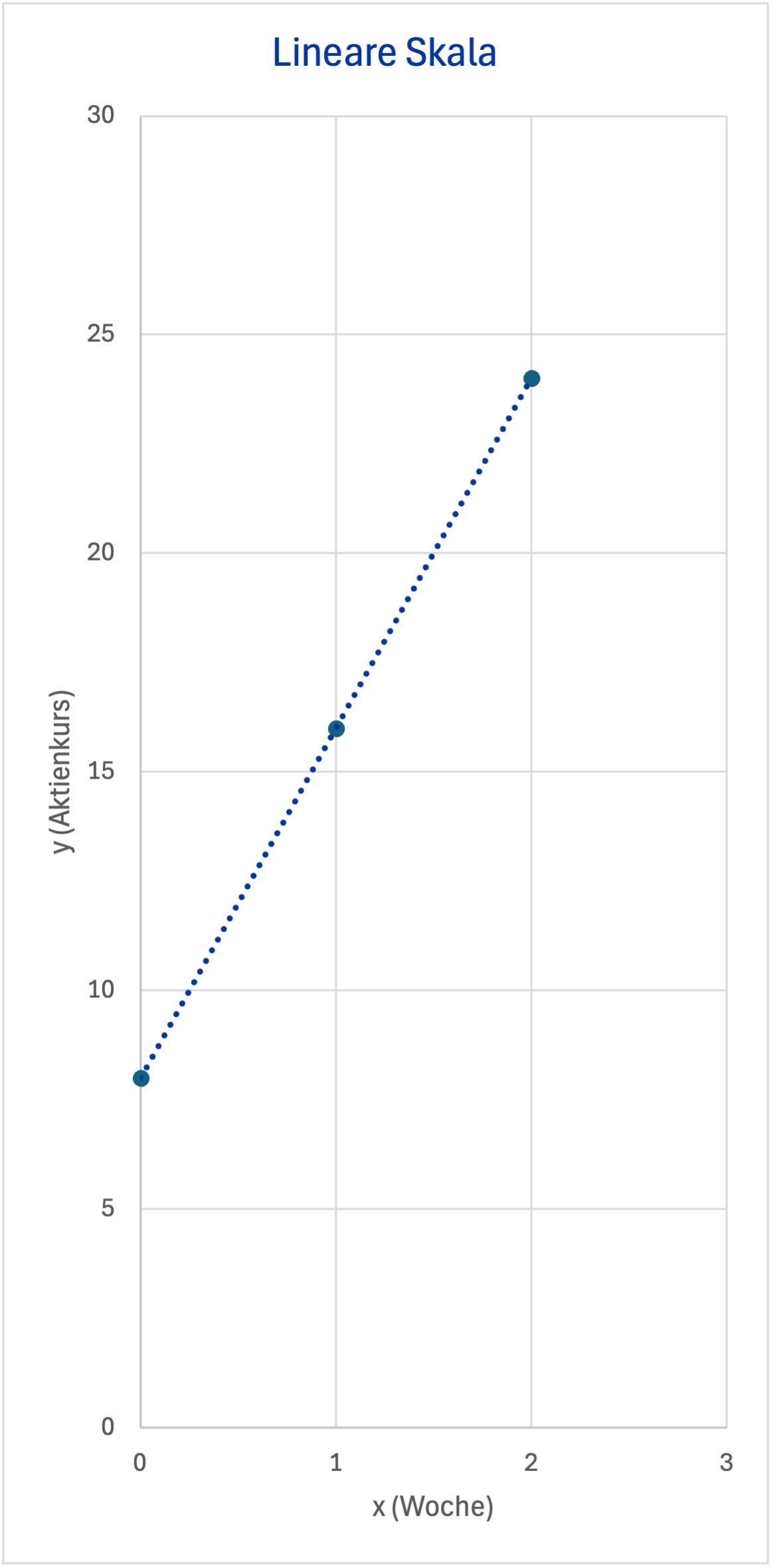
Angenommen, in einem Diagramm werden die Wochen auf der waagrechten x-Achse und die Kurse auf der senkrechten y-Achse abgetragen (lineare Skala mit gleichen Abständen zwischen 8 €, 16 €, 24 € ...).
Dann sieht die Kurssteigerung von 8 € auf 16 € genauso groß aus wie die Kurssteigerung von 16 € auf 24 € (in €-Beträgen ist sie das ja auch), der Graph ist eine Gerade. Die erste Steigung ist aber eine Verdopplung, die zweite nur eine Zunahme um 50 % – das geht in der linearen Skala unter.
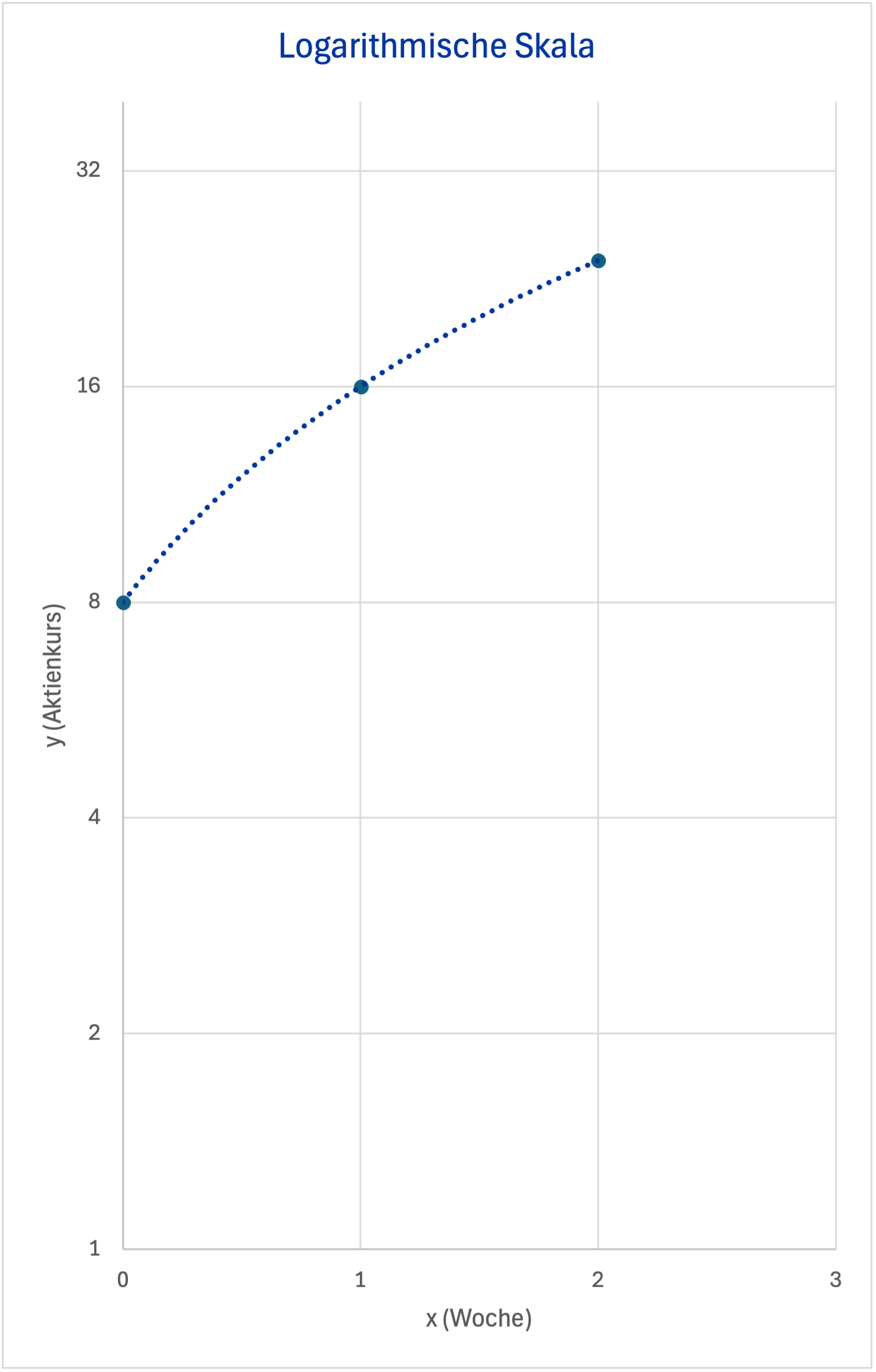
Auf einer logarithmischen Skala mit zum Beispiel dem Faktor 2 als Basis hingegen mit gleichen Abständen zwischen 1 €, 2 €, 4 €, 8 €, 16 €, 32 € und so weiter (also jeweils Verdoppelung) könnte man erkennen, dass die relative Kurssteigerung in der zweiten Woche abflacht und der Aktionär in der zweiten Woche viel weniger reich wird als in der ersten Woche.
Weitere Anwendungen und Varianten
Logarithmische Skalen werden mitunter auch einfach verwendet, um große Änderungen (etwa über lange Zeiträume) überhaupt in einer Grafik unterzubringen (bei einer linearen Skala und einer Verdreißigfachung beispielsweise des Aktienkurses, des Umsatzes oder des Bruttoinlandsprodukts würde der Graph sonst "oben aus dem Blatt laufen").
Oft sagt man auch halblogarithmische Darstellung, weil in der Regel nur die y-Achse logarithmisch skaliert ist.
Wird auch die x-Achse logarithmisch dargestellt, wird das durch den Begriff doppelt logarithmisch kenntlich gemacht.
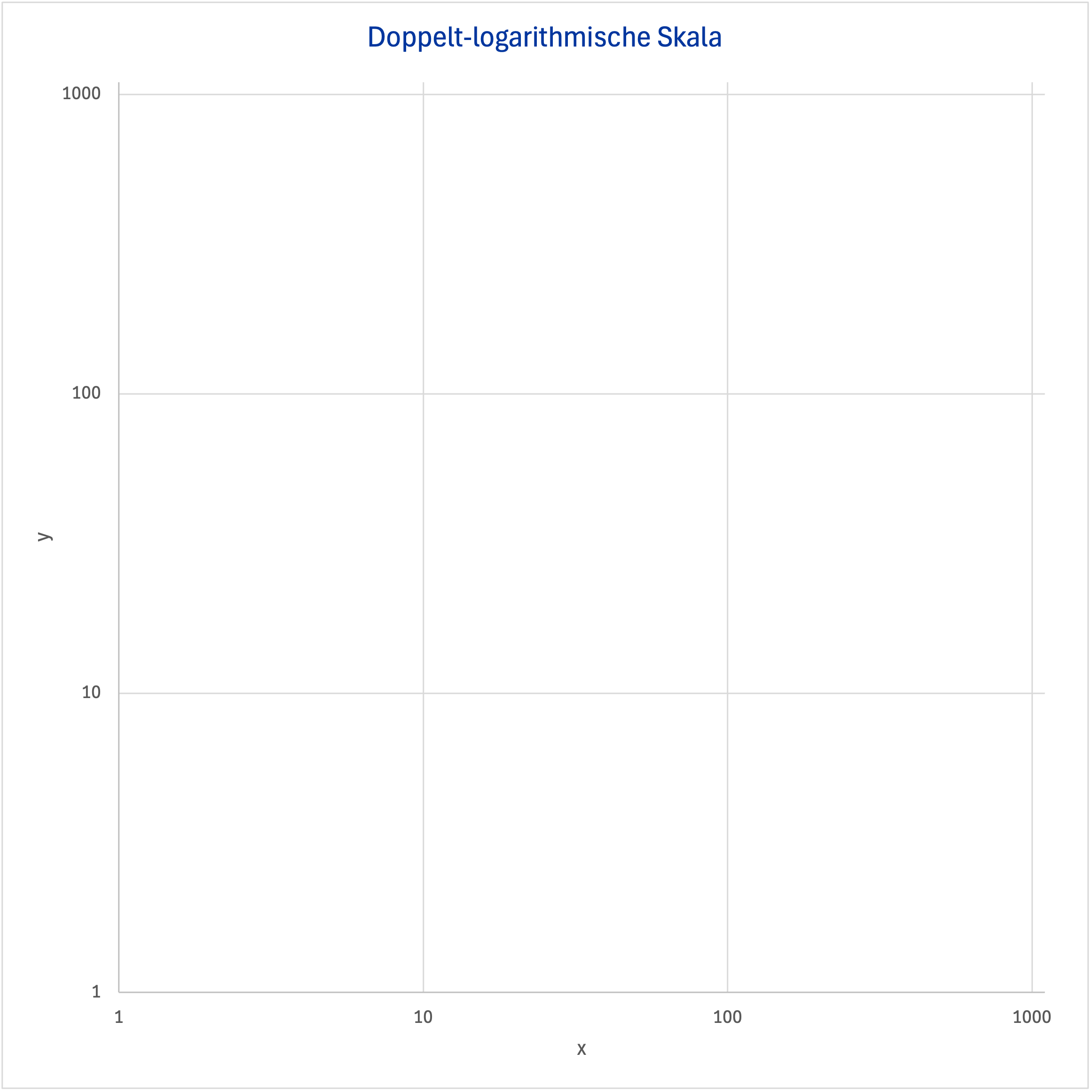
Beispiel: Doppelt-logarithmische Skala
Eine doppelt-logarithmische Skala auf Basis des Faktors 10 (also jeweils eine Verzehnfachung je Stufe) sieht so aus (hier ohne Werte):