Mittlere absolute Abweichung
Mittlere absolute Abweichung Definition
Die mittlere absolute Abweichung als ein Streuungsparameter misst die durchschnittliche absolute Abweichung vom arithmetischen Mittelwert (oder vom Median).
Es wird mit absoluten Abweichungen gerechnet, da sich positive und negative Differenzen sonst ausgleichen würden (einen ähnlichen Weg geht die Varianz, welche die Differenzen quadriert, um positive Werte zu erhalten).
Beispiel: mittlere absolute Abweichung berechnen
Auf Basis der Beispieldaten zum Median: Eine Familie hat 5 Kinder im Alter von 1, 3, 5, 9 und 12 Jahren. Der arithmetische Mittelwert, der in einem ersten Schritt berechnet werden muss, ist (1 + 3 + 5 + 9 + 12) / 5 = 30 / 5 = 6.
Die mittlere absolute Abweichung ist: ( | 1-6 | + | 3-6 | + | 5-6 | + | 9-6 | + | 12-6 | ) / 5 = (5 + 3 + 1 + 3 + 6) / 5 = 18 / 5 = 3,6.
Die mittlere absolute Abweichung von 3,6 (Jahren) vom Mittelwert von 6 (Jahren) spiegelt die Streuung der Altersdaten schon ganz gut wider. Als Grafik:
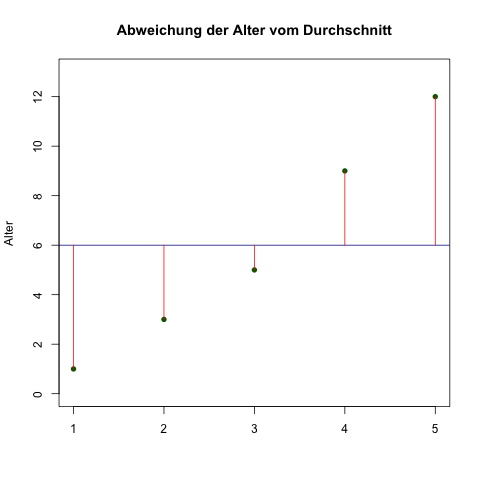
Angenommen, eine andere Familie hat ebenfalls 5 Kinder und zwar 2 Zwillingspärchen im Alter von 4 und 8 Jahren und ein Kind im Alter von 6 Jahren.
Dann ist das Durchschnittsalter ebenfalls 6 Jahre (Berechnung: (2 × 4 + 2 × 8 + 6) / 5 = 30/5 = 6), die mittlere absolute Abweichung ist jedoch: ( 2 × | 4-6 | + | 6-6 | + 2 × | 8-6 | ) / 5 = (4 + 0 + 4) / 5 = 8 / 5 = 1,6.
Die mit 1,6 im Vergleich zu 3,6 wesentlich niedrigere mittlere absolute Abweichung zeigt an, dass die Daten (Alter) viel näher beieinander liegen und weder nach oben noch nach unten wesentlich vom Mittelwert abweichen.
Oben haben wir die mittlere absolute Abweichung vom arithmetischen Mittelwert berechnet, es gibt aber auch eine mittlere absolute Abweichung vom Median.
Der Median ist der mittlere Wert, der die sortierte Reihe in der Mitte teilt. Das ist bei der ersten Familie mit 5 Kindern im Alter von 1, 3, 5, 9 und 12 Jahren der Wert 5 Jahre (das ist die Mitte; zwei (1 und 3 Jahre) liegen darunter, zwei (9 und 12 Jahre) darüber).
Die weitere Berechnung ist dann identisch. Die mittlere absolute Abweichung vom Median ist: ( | 1-5 | + | 3-5 | + | 5-5 | + | 9-5 | + | 12-5 | ) / 5 = (4 + 2 + 0 + 4 + 7) / 5 = 17 / 5 = 3,4.
Die mittlere absolute Abweichung ist nicht das Standardmaß für Streuung – das sind eher Varianz bzw. Standardabweichung.
Alternative Begriffe: durchschnittliche absolute Abweichung, durchschnittliche Abweichung, mittlere Abweichung, mittlere lineare Abweichung.