Normale
Normale Definition
Eine Normale ist eine Gerade, die in einem bestimmten Punkt senkrecht zur Tangente einer Funktion steht.
Die Normale wird durch eine Normalengleichung beschrieben. Wie für jede Gerade braucht man dazu 1) eine Steigung und 2) einen y-Achsenabschnitt.
Die Steigung der Normalen ist der negative Kehrwert der Tangentensteigung.
Beispiel
Beispiel: Normalengleichung aufstellen
Im Beispiel zur Tangente war die Tangentengleichung t(x) = 4x - 1 und der Berührpunkt war (1, 3), also x = 1 und y = 3.
Wenn die Steigung der Tangente wie hier 4 ist (das ist relativ steil: 1 cm nach rechts führt zu 4 cm nach oben), ist die (negative) Steigung der Normalen -1/4 (die Normale fällt relativ flach ab: 1 cm nach rechts führt zu 0,25 cm nach unten).
Die Normalengleichung ist allgemein:
$$n(x) = \frac{-1}{m_t} \cdot x + b$$
Dabei ist $m_t$ die Steigung der Tangente und $\frac{-1}{m_t}$ dann die Steigung der Normalen, b ist der (noch unbekannte) y-Achsenabschnitt.
Um diesen zu berechnen, werden die Koordinaten des Berührpunktes eingesetzt:
$$3 = \frac{-1}{4} \cdot 1 + b$$
b = 3,25
Der y-Achsenabschnitt ist also b = 3,25.
Die Normalengleichung ist dann:
$$n(x) = -\frac{1}{4} \cdot x + 3,25$$
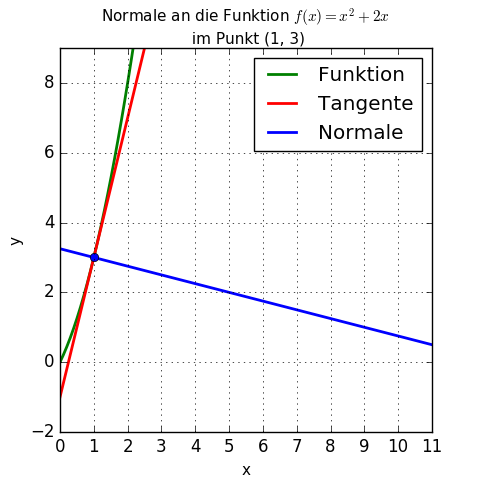
In der Grafik: