Differentialrechnung
Differentialrechnung Definition
Die Differentialrechnung berechnet, wie Funktionen sich verändern bzw. wie zusammenhängende Größen sich entwickeln.
Beispiele
Wie ändert sich die Nachfrage nach einem Produkt, wenn der Preis steigt (oder fällt)?
Wie ändert sich der Benzinverbrauch eines Autos, wenn man die Geschwindigkeit erhöht?
Die jeweilige Antwort hängt davon ab, ob es sich um eine lineare, eine exponentielle, eine logarithmische, eine zusammengesetzte Funktion usw. handelt.
Einordnung
Differentialrechnung und Integralrechnung bilden die Infinitesimalrechnung als ein Teilgebiet der Analysis.
Vorgehen: Ableitung bestimmen
Um die Änderungsraten zu bestimmen, berechnet man die Ableitung der jeweiligen Funktion.
Ist die 1. Ableitung einer Funktion an einer Stelle, in einem Intervall oder überall > 0, steigt die Funktion dort, das heißt die y-Werte nehmen mit zunehmenden x-Werten zu.
Ist die 1. Ableitung einer Funktion an einer Stelle, in einem Intervall oder überall < 0, fällt die Funktion dort, das heißt die y-Werte nehmen mit zunehmenden x-Werten ab.
Besonders interessant sind die Punkte, an denen die 1. Ableitung einer Funktion = 0 ist. Die Funktion steigt dort nicht (weiter), sie fällt dort nicht (weiter) – das könnte zum Beispiel der höchste Punkt (Maximum) oder der tiefste Punkt (Minimum) sein.
Beispiel
Beispiel: Differentialrechnung anwenden
Die untere Grafik zeigt die Funktion f(x) = x2.
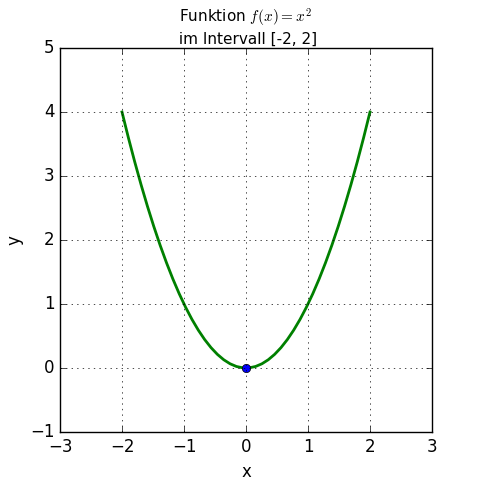
Die 1. Ableitung der Funktion ist f'(x) = 2x.
Für negative x ist 2x < 0, die Funktion fällt in diesem Bereich.
Für positive x ist 2x > 0, die Funktion steigt in diesem Bereich.
Für x = 0 ist 2x ebenfalls = 0, für unsere Funktion liegt hier ein Tiefpunkt bzw. ein Minimum vor (es könnte aber in anderen Fällen auch ein Maximum oder Sattelpunkt sein, dafür sind rechnerisch weitere Kriterien zu prüfen, wenn man es nicht in einer Grafik wie hier sehen kann).
Interpretation
Mit der Differentialrechnung kann man also (genau) beschreiben und berechnen, was man in einem Funktionsgraphen zumindest ungefähr sieht:
- Wo steigt und fällt eine Funktion?
- Mit welcher Änderungsrate (wächst eine Funktion stark oder schwach)?
- Wo gibt es Minima oder Maxima der Funktion?