Tangente
Tangente Definition
Eine Tangente ist eine Gerade, die eine Funktionskurve in einem bestimmten Punkt (z.B. der Punkt (1, 1) im Koordinatensystem) berührt (nicht schneidet).
Die Tangente hat dieselbe Steigung wie die Kurve (und das ist nützlich, da man so die Steigung bzw. die Änderungsrate einer nicht-linearen Funktion in einem Punkt bestimmen oder umgekehrt die Tangente berechnen kann).
Tangente berechnen
Für eine Funktion kann man die Tangente bzw. die Gleichung der Tangente wie folgt berechnen:
Beispiel: Tangente berechnen
Die Funktion sei f(x) = x2 + 2x.
Es soll die Gleichung der Tangente berechnet werden, welche die Kurve der Funktion im Punkt x = 1 berührt.
Zunächst x = 1 in die Funktion einsetzen: f(1) = 12 + 2 × 1 = 1 + 2 = 3.
D.h., die Tangente berührt die Funktionskurve im Punkt (1, 3), also x = 1 und y = 3.
Tangentensteigung berechnen
Nun muss noch die Steigung der Tangente berechnet werden:
1. Ableitung der Funktion bilden: f '(x) = 2x + 2.
f '(x) für x = 1 berechnen: f '(1) = 2 × 1 + 2 = 2 + 2 = 4. Das ist die Steigung.
(Hier macht man sich zunutze, dass die Steigung der Funktion (die 1. Ableitung) der Steigung der Tangente entspricht.)
Allgemein hat eine Gerade (damit auch die Tangente) die Form y = m × x + b (vgl. Lineare-Funktion).
Dabei ist m die Steigung (also 4, wie oben berechnet), x = 1 (vorgegeben) und y = 3 (oben berechnet); b (der Schnittpunkt mit der y-Achse) ist noch unbekannt.
Eingesetzt in die Geradengleichung:
3 = 4 × 1 + b
3 = 4 + b
Daraus folgt, dass b = -1 ist.
Tangentengleichung aufstellen
Die Tangentengleichung kann man mit t(x) bezeichnen, sie lautet dann: t (x) = 4 × x - 1.
Tangente zeichnen
Zum Zeichnen der Geraden könnte man z.B. 2 Punkte berechnen:
t (0) = 4 × 0 - 1 = -1
t (1) = 4 × 1 - 1 = 3
Und die Gerade durch die Punkte (0, -1) und (1, 3) laufen lassen.
Oder direkt die Gerade aus dem Punkt (1, 3) und der Steigung 4 konstruieren.
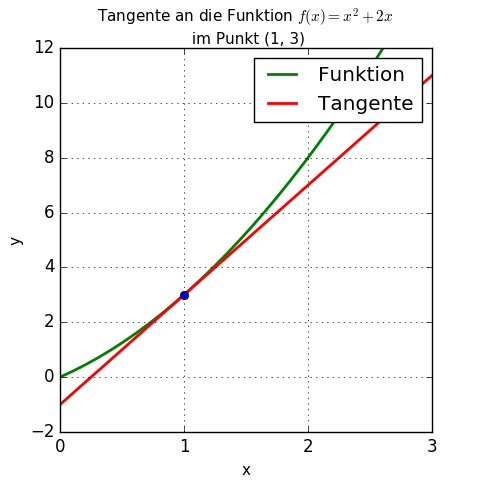
Die Steigung von 4 an der Stelle x = 1 bedeutet, dass sich der Funktionswert f(x) um das Vierfache des Wertes erhöht, um den man x (marginal) erhöht:
f(1,01) = 1,012 + 2 × 1,01 = 3,0401; D.h., der Funktionswert steigt gerundet um 0,04 wenn der x-Wert um 0,01 steigt. Die Änderungsrate der Funktion an der Stelle ist 4.
Waagerechte Tangente
Eine waagerechte / horizontale Tangente liegt vor, wenn die 1. Ableitung einer Funktion an einer Stelle x0 gleich 0 ist: f'(x0) = 0.
D.h., die Steigung ist an der Stelle 0.
In dem Punkt kann dann ein Maximum, ein Minimum oder ein Sattelpunkt liegen.