Normalverteilung
Normalverteilung Definition
Die Normalverteilung gehört zu den stetigen Verteilungen und bildet die Verteilung von Daten bzw. Häufigkeiten ab, wie sie in der Natur oft vorkommt. Die Normalverteilung ist symmetrisch um den Durchschnittswert bzw. Erwartungswert "aufgebaut".
Beispiel
Geht man davon aus, dass der deutsche Mann im Durchschnitt 1,80 Meter groß ist, zeigt die Normalverteilung, dass viele Männer um diesen Wert herum sind, z.B. 1,78 m, 1,79 m, 1,81 m oder 1,82 m. Viel weniger häufig sind 1,60 m oder 2,00 m etc.; die Symmetrie der Normalverteilung bedeutet, dass 1,79 m annähernd genauso häufig bzw. wahrscheinlich ist wie 1,81 m und 1,60 m genauso wahrscheinlich wie 2,00 m u.s.w.
Zeichnet man die Normalverteilung, indem man im Beispiel die Körpergröße auf der horizontalen x-Achse und die absolute oder relative Häufigkeit auf der vertikalen y-Achse abträgt, erhält man eine Glockenkurve (die Linie hat die Form einer Glocke).
Die Dicke / Breite der Glockenkurve wird durch die Varianz bestimmt. Erwartungswert und Varianz zusammen legen fest, um welchen Wert und mit welcher Breite die Glockenkurve aufgebaut ist; geschrieben wird dies als N(μ, σ2), z.B. N(1,80, 0,01), wenn der Mittelwert der Körpergröße von Männern 1,80 m und die Varianz 0,01 m2 (entspricht einer Standardabweichung von 0,1 m) wäre.
Die Dichtefunktion dieser Normalverteilung sieht so aus:
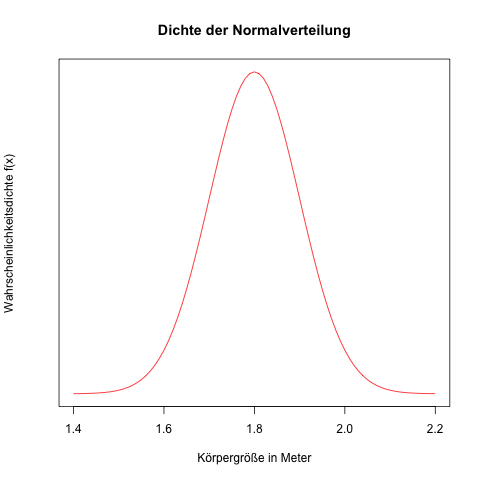
Dieses Wissen um die Normalverteilung kann man sich zunutze machen. Z.B. könnte sich ein Autohersteller fragen, wie die Sitze und die Deckenhöhe im Auto sein müssen, damit ein möglichst hoher Prozentsatz der Bevölkerung / der Autokäufer bequem sitzen kann, ohne anzustoßen; ebenso bei Konfektionsware.
Die Bedeutung der Normalverteilung als wichtigste Verteilung resultiert v.a. auch aus dem Zentralen Grenzwertsatz, wonach aus Stichproben gewonnene Daten wie z.B. der Mittelwert sich mit zunehmendem Stichprobenumfang der Normalverteilung annähern.
Aufgrund der Symmetrie der Normalverteilung sind Mittelwert/Erwartungswert, Median und Modalwert identisch.
Alternative Begriffe: Gauß-Kurve, Gauß-Verteilung, Gaußsche Kurve, Gaußsche Normalverteilung, Gaußsche Glockenkurve, Gaußsche Verteilung, Gaußverteilung, Normalverteilungskurve.
Standardbereiche
Für die Normalverteilung gilt:
- 68,3 % der Daten liegen in dem Bereich Mittelwert +/- Standardabweichung (im Beispiel oben: 1,70 m bis 1,90 m);
- 95,5 % der Daten liegen in dem Bereich Mittelwert +/- 2 mal Standardabweichung (im Beispiel oben: 1,60 m bis 2,00 m);
- 99,7 % der Daten liegen in dem Bereich Mittelwert +/- 3 mal Standardabweichung (im Beispiel oben: 1,50 m bis 2,10 m); d.h. nur 0,15 % liegen unter 1,50 m und nur 0,15 % über 2,10 m (bei 30 Mio. erwachsenen Männern wären dies jeweils 45.000).
Anwendungsgebiete
Die Normalverteilung ist nicht auf biologische Größen beschränkt, sondern kann eventuell in vielen anderen Bereichen angewendet werden:
- Nutzungsdauerabschätzung: wenn ein PKW z.B. im Regelfall 12 Jahre hält, dann liegen viele PKW um diesen Wert herum, halten also 11 oder 13 Jahre, 10 oder 14 Jahre etc., aber nur sehr wenige gehen nach einem Jahr kaputt und nur wenige halten länger als 20 Jahre;
- Qualitätskontrolle: wenn ein bestimmtes Brett in einer Möbelfabrik mit einer Dicke von 5 cm produziert werden soll, dann werden die meisten auch 5 cm sein und viele weichen nur wenig davon ab, z.B. 4,99 cm oder 5,02 cm etc.; je weiter man sich von den 5 cm nach oben oder unten entfernt, desto unwahrscheinlicher/seltener treten die Fälle auf (es wird kaum Bretter mit 1 cm geben).
Auch hier kann die Normalverteilung gegeben sein und für eine Analyse genutzt werden.