Standardnormalverteilung
Standardnormalverteilung Definition
Die Standardnormalverteilung ist eine Normalverteilung, bei der Mittelwert und Erwartungswert = 0 und die Varianz sowie Standardabweichung = 1 sind.
Diese Standardnormalverteilung ist i.d.R. nicht in der Realität gegeben (z.B. ist der Mittelwert der normalverteilten Variablen "Körpergröße von Männern" natürlich nicht 0, sondern eher 1,80 m), aber durch eine einfache z-Transformation kann jede Normalverteilung in eine Standardnormalverteilung überführt werden, für die dann Wahrscheinlichkeitswerte aus der entsprechenden Standardnormalverteilung-Tabelle abgelesen werden können (und somit nicht berechnet werden müssen).
Alternative Begriffe: N(0, 1) - Normalverteilung, standardisierte Normalverteilung, Standardverteilung.
Beispiel
Beispiel Standardnormalverteilung
Für die normalverteilte Variable "Körpergröße von Männern" eines Landes sind die Parameter Erwartungswert = 1,80 m und Standardabweichung = 0,1 m bekannt.
Wenn man z.B. wissen möchte, wie hoch der Anteil der Männer mit einer Körpergröße von mehr als 1,95 m ist, nimmt man zunächst die z-Transformation bzw. Standardisierung vor:
z = (1,95 m - 1,80 m) / 0,1 m = 0,15 m / 0,1 m = 1,5.
In der Standardnormalverteilung-Tabelle kann man den Wert für 1,5 ablesen: 0,933193. D.h., gut 93,3 % der Männer liegen bzgl. der Körpergröße im Bereich bis 1,95 m und 1 - 0,933193 = 0,066807 = gerundet 6,7 % sind über 1,95 m.
Einem 1,95 m großen Mann würde man sagen: "Sie liegen auf dem 93. Perzentil." (dann weiß er, dass nur ca. 7 % der Bevölkerung größer sind).
In einem anderen Land wären die Männer vielleicht größer oder kleiner und Erwartungswert und Standardabweichung entsprechend anders; Die Verteilung lässt sich aber analog auf eine Standardnormalverteilung zurückführen.
Standardnormalverteilung-Tabelle
So findet man einen gesuchten Wert in der Tabelle der Standardnormalverteilung bzw. z-Wert-Tabelle (hier auf 6 Nachkommastellen gerundet): im Beispiel wurde der z-Wert 1,5 gesucht; man nimmt die Zeile, die mit 1,5 beginnt und sieht in der Spalte 0,00 nach, der gesuchte Werte kann dort abgelesen werden mit 0,933193.
| 0,00 | 0,01 | 0,02 | 0,03 | 0,04 | 0,05 | 0,06 | 0,07 | 0,08 | 0,09 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0,0 | 0,500000 | 0,503989 | 0,507978 | 0,511967 | 0,515953 | 0,519939 | 0,523922 | 0,527903 | 0,531881 | 0,535856 |
| 0,1 | 0,539828 | 0,543795 | 0,547758 | 0,551717 | 0,555670 | 0,559618 | 0,563559 | 0,567495 | 0,571424 | 0,575345 |
| 0,2 | 0,579260 | 0,583166 | 0,587064 | 0,590954 | 0,594835 | 0,598706 | 0,602568 | 0,606420 | 0,610261 | 0,614092 |
| 0,3 | 0,617911 | 0,621719 | 0,625516 | 0,629300 | 0,633072 | 0,636831 | 0,640576 | 0,644309 | 0,648027 | 0,651732 |
| 0,4 | 0,655422 | 0,659097 | 0,662757 | 0,666402 | 0,670031 | 0,673645 | 0,677242 | 0,680822 | 0,684386 | 0,687933 |
| 0,5 | 0,691462 | 0,694974 | 0,698468 | 0,701944 | 0,705402 | 0,708840 | 0,712260 | 0,715661 | 0,719043 | 0,722405 |
| 0,6 | 0,725747 | 0,729069 | 0,732371 | 0,735653 | 0,738914 | 0,742154 | 0,745373 | 0,748571 | 0,751748 | 0,754903 |
| 0,7 | 0,758036 | 0,761148 | 0,764238 | 0,767305 | 0,770350 | 0,773373 | 0,776373 | 0,779350 | 0,782305 | 0,785236 |
| 0,8 | 0,788145 | 0,791030 | 0,793892 | 0,796731 | 0,799546 | 0,802338 | 0,805106 | 0,807850 | 0,810570 | 0,813267 |
| 0,9 | 0,815940 | 0,818589 | 0,821214 | 0,823814 | 0,826391 | 0,828944 | 0,831472 | 0,833977 | 0,836457 | 0,838913 |
| 1,0 | 0,841345 | 0,843752 | 0,846136 | 0,848495 | 0,850830 | 0,853141 | 0,855428 | 0,857690 | 0,859929 | 0,862143 |
| 1,1 | 0,864334 | 0,866500 | 0,868643 | 0,870762 | 0,872857 | 0,874928 | 0,876976 | 0,878999 | 0,881000 | 0,882977 |
| 1,2 | 0,884930 | 0,886860 | 0,888767 | 0,890651 | 0,892512 | 0,894350 | 0,896165 | 0,897958 | 0,899727 | 0,901475 |
| 1,3 | 0,903199 | 0,904902 | 0,906582 | 0,908241 | 0,909877 | 0,911492 | 0,913085 | 0,914656 | 0,916207 | 0,917736 |
| 1,4 | 0,919243 | 0,920730 | 0,922196 | 0,923641 | 0,925066 | 0,926471 | 0,927855 | 0,929219 | 0,930563 | 0,931888 |
| 1,5 | 0,933193 | 0,934478 | 0,935744 | 0,936992 | 0,938220 | 0,939429 | 0,940620 | 0,941792 | 0,942947 | 0,944083 |
| 1,6 | 0,945201 | 0,946301 | 0,947384 | 0,948449 | 0,949497 | 0,950529 | 0,951543 | 0,952540 | 0,953521 | 0,954486 |
| 1,7 | 0,955435 | 0,956367 | 0,957284 | 0,958185 | 0,959071 | 0,959941 | 0,960796 | 0,961636 | 0,962462 | 0,963273 |
| 1,8 | 0,964070 | 0,964852 | 0,965621 | 0,966375 | 0,967116 | 0,967843 | 0,968557 | 0,969258 | 0,969946 | 0,970621 |
| 1,9 | 0,971284 | 0,971933 | 0,972571 | 0,973197 | 0,973810 | 0,974412 | 0,975002 | 0,975581 | 0,976148 | 0,976705 |
| 2,0 | 0,977250 | 0,977784 | 0,978308 | 0,978822 | 0,979325 | 0,979818 | 0,980301 | 0,980774 | 0,981237 | 0,981691 |
| 2,1 | 0,982136 | 0,982571 | 0,982997 | 0,983414 | 0,983823 | 0,984222 | 0,984614 | 0,984997 | 0,985371 | 0,985738 |
| 2,2 | 0,986097 | 0,986447 | 0,986791 | 0,987126 | 0,987455 | 0,987776 | 0,988089 | 0,988396 | 0,988696 | 0,988989 |
| 2,3 | 0,989276 | 0,989556 | 0,989830 | 0,990097 | 0,990358 | 0,990613 | 0,990863 | 0,991106 | 0,991344 | 0,991576 |
| 2,4 | 0,991802 | 0,992024 | 0,992240 | 0,992451 | 0,992656 | 0,992857 | 0,993053 | 0,993244 | 0,993431 | 0,993613 |
| 2,5 | 0,993790 | 0,993963 | 0,994132 | 0,994297 | 0,994457 | 0,994614 | 0,994766 | 0,994915 | 0,995060 | 0,995201 |
| 2,6 | 0,995339 | 0,995473 | 0,995603 | 0,995731 | 0,995855 | 0,995975 | 0,996093 | 0,996207 | 0,996319 | 0,996427 |
| 2,7 | 0,996533 | 0,996636 | 0,996736 | 0,996833 | 0,996928 | 0,997020 | 0,997110 | 0,997197 | 0,997282 | 0,997365 |
| 2,8 | 0,997445 | 0,997523 | 0,997599 | 0,997673 | 0,997744 | 0,997814 | 0,997882 | 0,997948 | 0,998012 | 0,998074 |
| 2,9 | 0,998134 | 0,998193 | 0,998250 | 0,998305 | 0,998359 | 0,998411 | 0,998462 | 0,998511 | 0,998559 | 0,998605 |
| 3,0 | 0,998650 | 0,998694 | 0,998736 | 0,998777 | 0,998817 | 0,998856 | 0,998893 | 0,998930 | 0,998965 | 0,998999 |
| 3,1 | 0,999032 | 0,999064 | 0,999096 | 0,999126 | 0,999155 | 0,999184 | 0,999211 | 0,999238 | 0,999264 | 0,999289 |
| 3,2 | 0,999313 | 0,999336 | 0,999359 | 0,999381 | 0,999402 | 0,999423 | 0,999443 | 0,999462 | 0,999481 | 0,999499 |
| 3,3 | 0,999517 | 0,999533 | 0,999550 | 0,999566 | 0,999581 | 0,999596 | 0,999610 | 0,999624 | 0,999638 | 0,999650 |
| 3,4 | 0,999663 | 0,999675 | 0,999687 | 0,999698 | 0,999709 | 0,999720 | 0,999730 | 0,999740 | 0,999749 | 0,999758 |
| 3,5 | 0,999767 | 0,999776 | 0,999784 | 0,999792 | 0,999800 | 0,999807 | 0,999815 | 0,999821 | 0,999828 | 0,999835 |
| 3,6 | 0,999841 | 0,999847 | 0,999853 | 0,999858 | 0,999864 | 0,999869 | 0,999874 | 0,999879 | 0,999883 | 0,999888 |
Die Tabelle zeigt die kumulierten Wahrscheinlichkeiten bis zu dem jeweiligen Wert, z.B. für den Wert 2,5 die kumulierte Wahrscheinlichkeit 0,993790.
Möchte man die Wahrscheinlichkeit berechnen, dass die standardnormalverteilte Zufallsvariable > 2,5 ist, muss man rechnen: 1 - 0,993790 = 0,00621 (ca. 0,62 %).
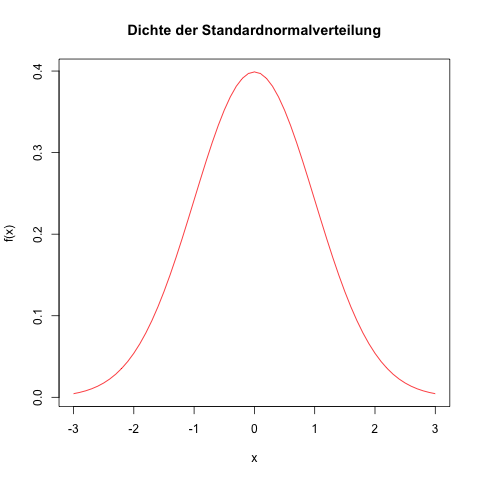
Dichte der Standardnormalverteilung
Die Dichte f(x) der Standardnormalverteilung sieht so aus (Glockenkurve):
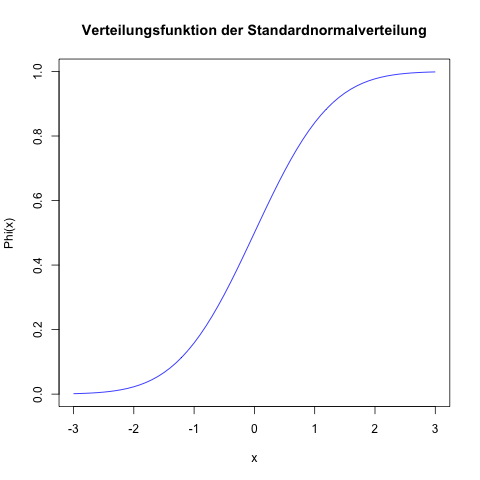
Verteilungsfunktion der Standardnormalverteilung
Die Verteilungsfunktion φ(x) – mit φ als der griechische Buchstabe Phi – der Standardnormalverteilung sieht so aus: