Ortsvektor
Ortsvektor Definition
Hat man zum Beispiel einen Punkt A mit den Koordinaten A (2, 3) – also vom Ursprung aus 2 cm (oder eine andere Einheit) auf der x-Achse nach rechts und 3 cm auf der y-Achse nach oben –, gibt es zu diesem Punkt einen Ortsvektor.
Dieser geht vom Koordinatenursprung (0, 0) zu dem Punkt A; Schreibweise:
$$\vec a = \overrightarrow {0A} = \begin{pmatrix} 2 \\ 3 \end{pmatrix}$$
Grafisch:
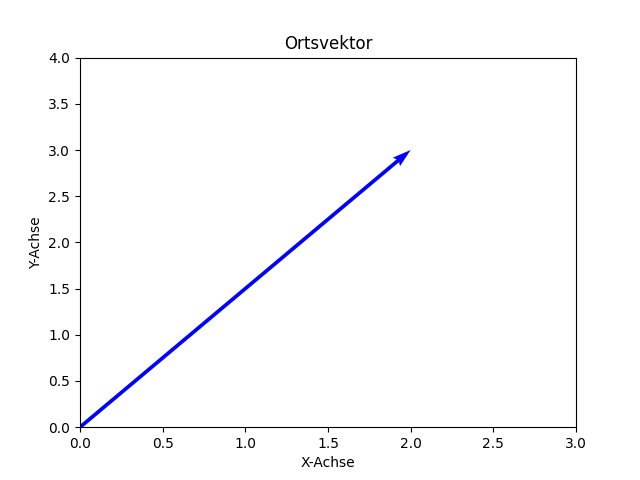
Analog im dreidimensionalen Raum: hat man hier einen Punkt mit den Koordinaten B (2, 3, 1) – also 2 cm auf der x-Achse nach rechts, 3 cm auf der y-Achse nach oben und 1 cm auf der z-Achse nach vorne –, gibt es zu diesem Punkt den Ortsvektor $\vec b$:
$$\vec b = \overrightarrow {0B} = \begin{pmatrix} 2 \\ 3 \\ 1 \end{pmatrix}$$
Hinweis
Man muss hier etwas aufpassen, wie das dreidimensionale Koordinatensystem definiert ist; teilweise werden die Achsen statt mit x, y und z auch mit x1, x2 und x3 bezeichnet und es wird anders bestimmt, welche Achse waagrecht, welche senkrecht und welche im Raum nach vorne bzw. hinten geht.