Symmetrie von Funktionen
Symmetrie von Funktionen Definition
Die Symmetrie ist eine weitere mögliche Eigenschaft einer Funktion.
Funktionen können punktsymmetrisch oder achsensymmetrisch sein.
Alternative Begriffe: Symmetrieverhalten.
Beispiele
Beispiel 1: Punktsymmetrie
Punktsymmetrie bedeutet: es gibt einen Punkt, an dem gespiegelt eine Funktion dieselbe Funktion ergibt; ist dieser Punkt der Ursprung / Nullpunkt des Koordinatensystems, gilt: f(-x) = -f(x).
Das ist zum Beispiel bei der Funktion f(x) = x3 so: f(-2) = -23 = -8. Das ist gleich -f(2) = - 23 = - 8.
Alternative Formel: f(x) = -f(-x), also 23 = - -23 = 8.
Die Funktion nennt man dann ungerade Funktion.
Der Graph der Funktion – die kubische Parabel – zeigt die Punktsymmetrie:
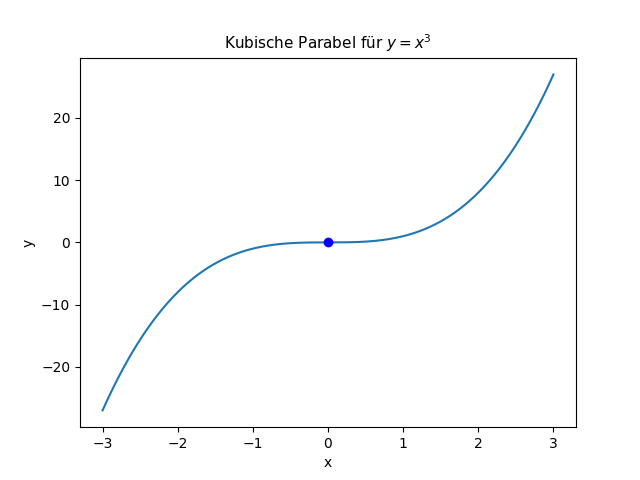
Beispiel 2: Achsensymmetrie
Achsensymmetrie bedeutet: es gibt eine Gerade / Achse, an der gespiegelt eine Funktion dieselbe Funktion ergibt (Spiegelsymmetrie); ist diese Gerade die y-Achse, gilt: f(-x) = f(x).
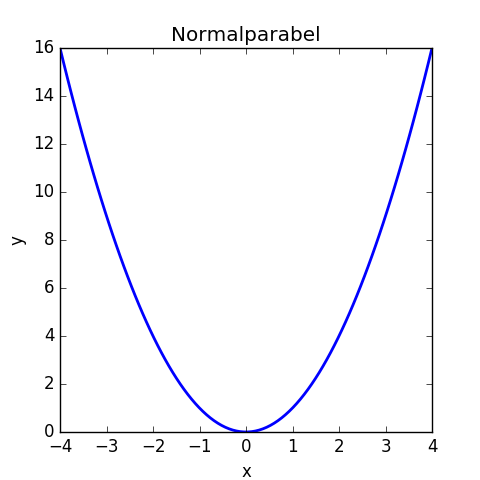
Das ist zum Beispiel bei der Funktion f(x) = x2 so: f(-2) = -22 = 4. Das ist gleich f(2) = 22 = 4.
Die Funktion nennt man dann gerade Funktion.
Der Graph der Funktion – die Normalparabel – zeigt die Achsensymmetrie: