Tangens
Tangens Definition
Der Tangens $tan (\alpha)$ ist eine Winkelfunktion: das Argument $\alpha$, das durch die Tangensfunktion verarbeitet wird, ist ein Winkel.
Tangens Formel
Der Tangens von $\alpha$ ist das Verhältnis von Gegenkathete zu Ankathete im rechtwinkligen Dreieck:
$$tan (\alpha) = \frac{Gegenkathete}{Ankathete}$$
Tangens Taschenrechner
Auf dem Taschenrechner gibt man den Winkel $\alpha$ in Grad ein (zum Beispiel 30°) und drückt die TAN-Taste; das Ergebnis für 30° ist gerundet 0,57735.
Das Verhältnis von Gegenkathete zu Ankathete ist somit 0,57735 (zum Beispiel ca. 5,77 cm zu 10 cm).
Das Ergebnis der Tangensfunktion – das Verhältnis von Gegenkathete zu Ankathete – ist nur vom Winkel abhängig und unabhängig von der Größe des Dreiecks.
Beispiel
Beispiel: Tangens berechnen
Wir nutzen mal den oben mit dem Taschenrechner berechneten Wert von gerundet 0,577 für 30°, um daraus ein rechtwinkliges Dreieck zu zeichnen, das einen $\alpha$-Winkel von 30° hat.
Dazu zeichnen wird die Ankathete mit 10 cm ein und senkrecht dazu die Gegenkathete mit 5,77 cm.
Verbinden wir den Anfangspunkt der Ankathete mit dem Endpunkt der Gegenkathete, erhalten wir die dem rechten Winkel gegenüberliegende Hypotenuse.
Zwischen Ankathete und Hypotenuse ist der Winkel $\alpha$ mit 30°.
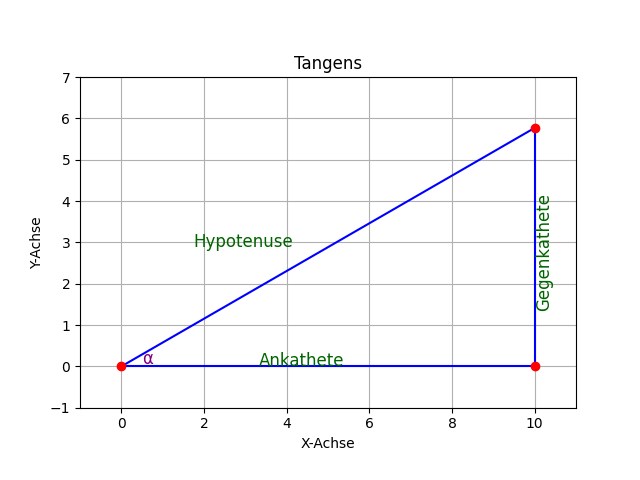
Um im Bild vom rechtwinkligen Dreieck zu bleiben: die Leiter (Hypotenuse) lehnt im 30° - Winkel an der Wand (Gegenkathete) an.
Nochmals als ursprüngliche Berechnung:
$$tan (\alpha) = \frac{Gegenkathete}{Ankathete}$$
$$= \frac{5.77}{10.00} = 0,577$$