Rechtwinkliges Dreieck

Rechtwinkliges Dreieck Definition

Lehnt man auf einer ebenen Fläche eine Leiter an eine Wand, bilden Leiter, Boden und Wand zweidimensional betrachtet ein rechtwinkliges Dreieck mit einem rechten Winkel (einem 90-Grad-Winkel) zwischen Wand und Boden.

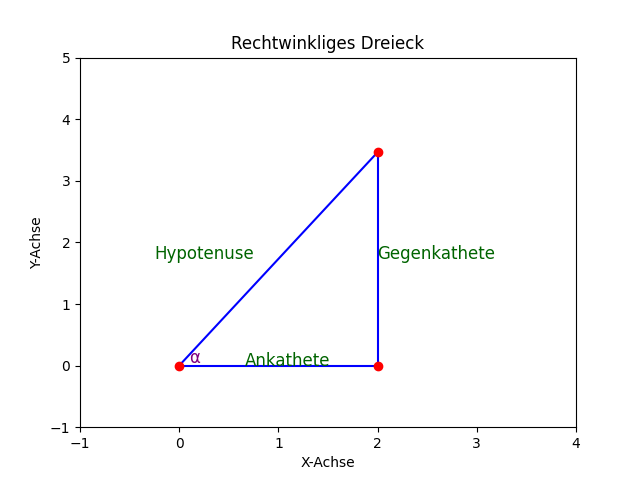
Die 3 Seiten: Ankathete, Gegenkathete und Hypotenuse

Bezeichnet man den Winkel zwischen Leiter und Boden mit $\alpha$, dann ist

• der Boden (zwischen Leiterfuß und Wand) die Ankathete (liegt am Winkel $\alpha$ an),
• die Wand (vom Boden bis zum Leiterende) die Gegenkathete (liegt dem Winkel $\alpha$ gegenüber) und
• die Leiter die Hypotenuse (liegt dem rechten Winkel gegenüber).

Grafisch:

Betrachtet man das rechtwinklige Dreieck hingegen aus Sicht des Winkels zwischen Leiter und Wand und bezeichnet diesen Winkel mit $\beta$, dann ist nunmehr die Wand die Ankathete, der Boden ist die Gegenkathete und die Leiter bleibt die Hypotenuse.

Mit diesen Begriffen werden dann die trigonometrischen Funktionen / Winkelfunktionen Sinus, Kosinus und Tangens definiert, welche die Längen von zwei dieser drei jeweils in ein Verhältnis setzen.

Winkelsummensatz

Im rechtwinkligen Dreieck gilt der Winkelsummensatz:

$$\alpha + \beta + 90° = 180°$$

$$\alpha + \beta = 90°$$

$\alpha$ und $\beta$ werden spitze Winkel (< 90°) genannt.

Die Verhältnisse der Dreiecksseiten zueinander (bei einem gegebenen Winkel) bleiben immer konstant. Verdoppelt man zum Beispiel die Seitenlänge der Ankathete, verdoppeln sich auch Gegenkathete und Hypotenuse.