Kosinus
Kosinus Definition
Der Kosinus bzw. Cosinus $cos (\alpha)$ ist eine Winkelfunktion: das Argument $\alpha$, das durch die Kosinusfunktion $y = cos (\alpha)$ verarbeitet wird, ist ein Winkel.
Formel
Der Kosinus von $\alpha$ ist das Verhältnis von Ankathete zu Hypotenuse im rechtwinkligen Dreieck:
$$cos (\alpha) = \frac{Ankathete}{Hypotenuse}$$
Beispiel
Beispiel: Kosinus berechnen
Auf dem Taschenrechner gibt man den Winkel in Grad ein (zum Beispiel 30°) und drückt die COS-Taste; das Ergebnis für 30° ist gerundet 0,866.
Das Verhältnis von Ankathete zu Hypotenuse ist somit 0,866 (zum Beispiel 8,66 cm zu 10 cm); das Ergebnis der Cosinusfunktion – das Verhältnis von Ankathete zu Hypotenuse – ist nur vom Winkel abhängig und unabhängig von der Größe des Dreiecks.
Bei 60° wäre des Cosinus beispielsweise 0,5, die Ankathete ist halb so lang wie die Hypotenuse.
Wir nutzen diesen mit dem Taschenrechner berechneten Wert von 0,5 für 60°, um daraus ein rechtwinkliges Dreieck zu zeichnen, das einen alpha-Winkel von 60° hat.
Wenn wir die Ankathete mit 4 cm ansetzten, wissen wir, dass die Hypotenuse 8 cm sein muss (da das Verhältnis von Ankathete zu Hypotenuse 0,5 ist).
Aus dem Satz des Pythagoras können wir dann die Gegenkathete berechnen:
(Hypotenuse)2 = (Ankathete)2 + (Gegenkathete)2
(Gegenkathete)2 = (Hypotenuse)2 - (Ankathete)2
(Gegenkathete)2 = 82 - 42 = 64 - 16 = 48.
Gegenkathete = Wurzel aus 48 = 6,928.
Das entsprechende rechtwinklige Dreieck dazu:
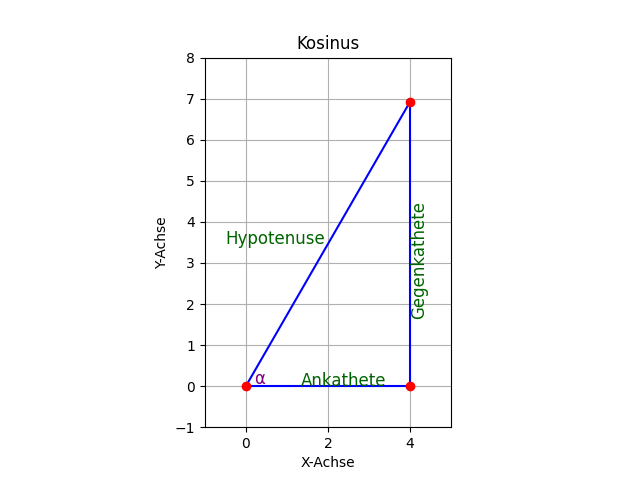
Die Ankathete ist 4 cm lang, die Gegenkathete 6,928 cm und die Hypotenuse 8 cm.
Zwischen Ankathete und Hypotenuse ist der Winkel alpha mit 60°.
Als ursprüngliche Berechnung:
$$cos (\alpha = 60°) = \frac{Ankathete}{Hypotenuse}$$
$$= \frac{4}{8} = 0,5$$