Asymptote
Asymptote Definition
Nähert sich der Graph einer Funktion bzw. ihre Kurve im Unendlichen (also für sehr große positive oder negative x) einer Geraden (manchmal auch Kurve) immer weiter an, nennt man diese Gerade (bzw. Kurve) Asymptote. Annähern heißt: nicht berühren.
Möglich sind waagrechte, senkrechte und schiefe bzw. schräge Asymptoten. Das Verhalten einer Funktion (bzw. deren Untersuchung) in diesen Grenzbereichen nennt man Asymptotik oder Asymptotisches Verhalten.
Beispiel: Asymptote e-Funktion
Die e-Funktion $f(x) = e^x$ strebt für x gegen plus unendlich gegen plus unendlich.
Die e-Funktion $f(x) = e^x$ strebt für x gegen minus unendlich gegen 0 (so ist bereits für x = -20 $f(x) = e^{-20}$ mit 0,000000002 nahe an Null).
Die e-Funktion hat deshalb eine waagrechte Asymptote bei der x-Achse bzw. y = 0 (Gleichung der Asymptote) für x gegen minus unendlich.
Alternative Begriffe: Asymptotik, Asymptotisches Verhalten.
Beispiel
Beispiel: Asymptote berechnen
Es liegt folgende gebrochen-rationale Funktion vor:
$$f(x) = \frac{x^2 - 1}{2x^2 + 4x}$$
Waagrechte Asymptote
Bei der Funktion ist der Grad (die höchste Potenz von x) des Zählerpolynoms x2 - 1 gleich 2, der Grad des Nennerpolynoms 2x2 + 4x ist ebenfalls gleich 2.
Ermittelt man nun die Koeffizienten (die Zahlen vor dem x2) noch mit a = 1 für den Zähler und b = 2 für den Nenner, liegt die waagrechte Asymptote bei y = a/b = 1/2 = 0,5 (eine Gerade, die auf Höhe 0,5 parallel zur x-Achse verläuft).
Das Ergebnis kann man prüfen, indem man mal x = 1.000.000 in die Funktion einsetzt (als Annäherung an unendlich und für den Taschenrechner noch machbar), man erhält f(1.000.000) = 0,499999.
Ist der Zählergrad < Nennergrad (z.B. wenn im Zähler ein x2 vorkommt und im Nenner ein x3), liegt die waagrechte Asymptote bei y = 0, d.h., die x-Achse ist die waagrechte Asymptote.
Senkrechte Asymptote
Um etwaige senkrechte Asymptoten zu finden, betrachtet man die Nullstellen des Nennerpolynoms.
Dazu kann man die Funktion zunächst faktorisieren:
$$f(x) = \frac{x^2 - 1}{2x^2 + 4x} = \frac{(x + 1) (x - 1)}{2x(x + 2)}$$
Der Bruch muss ggf. noch gekürzt werden (hier nicht).
Die Nullstellen des (faktorisierten) Nennerpolynoms kann man leicht erkennen: x1 = 0 und x2 = -2.
Es gibt somit zwei senkrechte Asymptoten: die bei x gleich 0 bzw. -2 parallel zur y-Achse verlaufenden Geraden.
In der Funktionsgrafik kann man die Annäherungen waagrecht bei y = 0,5 und senkrecht bei x = -2 und x = 0 erkennen:
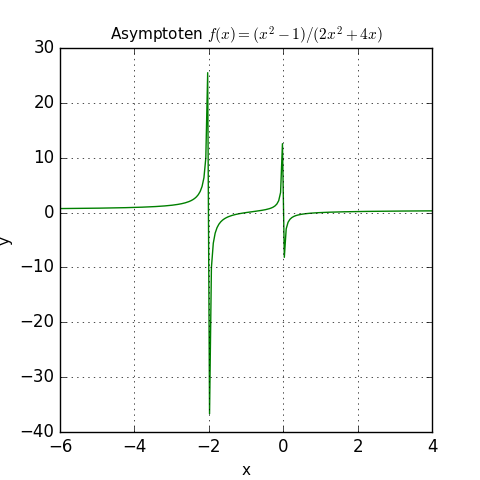
Schiefe / schräge Asymptote
Eine schiefe Asymptote wäre z.B. eine Gerade, die in einem 45-Grad-Winkel oder 20-Grad-Winkel steigt und an die sich eine andere Funktion annähert.