Doppelte Nullstelle

Beispiel

Die Funktion $(x - 1)^2$ kann man auch so schreiben: $(x - 1) \cdot (x - 1)$; sie hat eine doppelte Nullstelle bei x = 1.

Diese setzt den ersten Term (x - 1) gleich 0 und den zweiten Term (x - 1) ebenfalls.

Bedeutung

Sehen wir uns die obige Funktion als Graph an und erkennen daran Eigenschaften und Folgen einer doppelten Nullstelle:

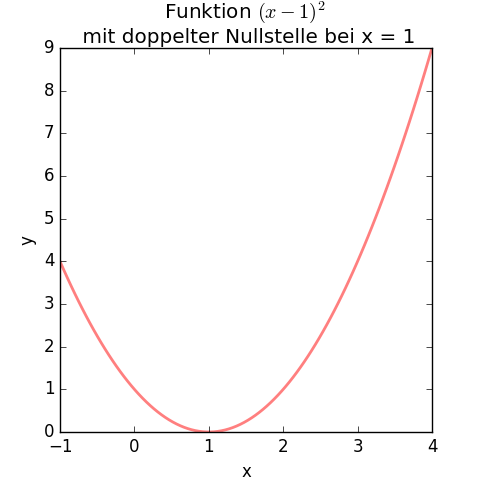
Berührpunkt

Hat eine Funktion eine doppelte Nullstelle, berührt ihr Funktionsgraph die waagrechte x-Achse (und schneidet sie nicht):

Extrempunkt

Wenn ein x (hier: x = 1) eine doppelte Nullstelle von f(x) ist, ist sie auch Nullstelle der Ableitung f'(x):

Die 1. Ableitung von $f(x) = (x - 1)^2$ ist (mit der Kettenregel abgeleitet):

$f'(x) = 2 \cdot (x - 1) \cdot 1 = 2x - 2$

Die Nullstelle dieser Ableitungsfunktion ist x = 1 ($2 \cdot 1 - 2 = 0$).

Es liegt deshalb ein Extrempunkt, das heißt ein Minimum oder Maximum vor.

Hier liegt ein Minimum vor.

Vorzeichenwechsel

Der Graph wechselt hier an den Nullstelle von positiven Funktionswerten zu wiederum positiven Funktionswerten (oder umgekehrt bei anderen Funktionen: von negativen Funktionswerten zu wiederum negativen Funktionswerten).

Abgrenzung zu einfacher Nullstelle

Bei einer einfachen Nullstelle wie im Beispiel zu Nullstellen schneidet der Graph die x-Achse, die Funktionswerte wechseln von positiv zu negativ oder umgekehrt von negativ zu positiv.