Krümmungsverhalten
Krümmungsverhalten Definition
Die Krümmung einer Funktion ergibt sich aus der zweiten Ableitung der Funktion.
Ist die 2. Ableitung f '' (x)
- > 0, ist die Funktion (bzw. ihr Graph) linksgekrümmt (konvex, positiv gekrümmt, Linkskurve), die Steigung nimmt zu; linksgekrümmt heißt: wenn man sich die Funktionskurve als Bobbahn vorstellt und man mit seinem Bob darin sitzt, würde man die Bobkufen nach links einschlagen bzw. lenken, um dem Verlauf der Linkskurve zu folgen.
- < 0, ist die Funktion rechtsgekrümmt (konkav, negativ gekrümmt, Rechtskurve), die Steigung nimmt ab; rechtsgekrümmt heißt: man schlägt die Bobkufen nach rechts ein bzw. lenkt rechts, um dem Verlauf der Bobbahn-Kurve zu folgen.
- = 0, ist die Funktion (an der Stelle) flach, die Steigung ist konstant.
Beispiel
Die zu untersuchende Funktion sei f (x) = x2 und der Definitionsbereich umfasse die positiven ganzen Zahlen. Setzt man z.B. die Werte 1, 2, 3 und 4 ein, erhält man als Funktionswerte f (x = 1) = 12 = 1; f (x = 2) = 22 = 4; f (x = 3) = 32 = 9; f (x = 4) = 42 = 16. Die Werte der Funktion nehmen mit steigenden x stark zu, die Steigung nimmt zu (die Tangente wird steiler).
Die 1. Ableitung der Funktion f'(x) ist 2x.
Die 2. Ableitung der Funktion f''(x) ist 2. Diese 2. Ableitung ist für alle x positiv (unverändert, immer 2), die Funktion ist linksgekrümmt bzw. konvex:
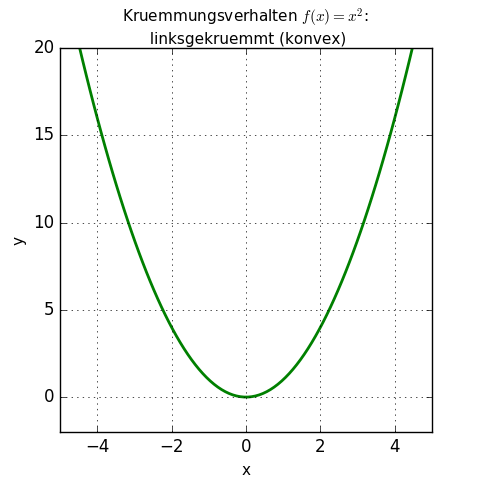
f''(x) > 0 bedeutet: die durch die 1. Ableitung repräsentierte (momentane) Änderungsrate nimmt zu.
Würde die Funktion f(x) = x2 die zurückgelegte Strecke abhängig von der Zeit darstellen (also z.B. 1 Meter nach 1 Sekunde, 4 Meter nach 2 Sekunden, 9 Meter nach 3 Sekunden usw.), wäre die 1. Ableitung die Geschwindigkeit und die 2. Ableitung die Beschleunigung. Ist diese 2. Ableitung an einem Punkt > 0, nimmt die Geschwindigkeit hier zu, es wird beschleunigt).
Eine Funktion kann aber auch konvexe und konkave Abschnitte (Intervalle) haben.
Alternative Begriffe: konkave Funktion, Konkavität, konvexe Funktion, Konvexität.