Wendepunkt
Wendepunkt Definition
Der Graph einer Funktion hat da einen Wendepunkt, wo sich sein Krümmungsverhalten ändert, zum Beispiel von einer konvexen Links- zu einer konkaven Rechtskrümmung.
Anzahl der Wendepunkte
Eine Funktion kann einen, mehrere oder auch keine Wendepunkte haben.
Bedingungen
Voraussetzung für einen Wendepunkt ist, dass die 2. Ableitung der Funktion (am Wendepunkt) gleich 0 und die 3. Ableitung ungleich 0 ist.
Alternative Begriffe: Krümmungsstelle, Wendestelle.
Beispiel
Beispiel: Wendepunkte berechnen
Die Funktion sei f(x) = x3.
Es werden nun die ersten drei Ableitungen der Funktion benötigt:
Die 1. Ableitung ist f '(x) = 3x2.
Die 2. Ableitung ist f ''(x) = 6x. Setzt man diese 2. Ableitung gleich 0 (also 6x = 0), ergibt dies x = 0. Bei x = 0 könnte ein Wendepunkt sein.
Die 3. Ableitung f '''(x) ist 6. Dann ist auch die 3. Ableitung an der Stelle 0, also f '''(0) = 6 und damit ungleich 0; deshalb ist bei x = 0 ein Wendepunkt der Funktion und y ist dann f(0) = 03 = 0 (wäre die 3. Ableitung an der Stelle gleich 0, läge kein Wendepunkt vor).
Rechts-Links-Wendepunkt oder Links-Rechts-Wendepunkt?
Die 3. Ableitung ist hier > 0; damit liegt ein Rechts-Links-Wendepunkt vor (von einer Rechts- in eine Linkskrümmung übergehend; man schlägt das Lenkrad bis zum Wendepunkt rechts und ab da dann links ein).
Ist die 3. Ableitung hingegen < 0; liegt ein Links-Rechts-Wendepunkt vor (von einer Links- in eine Rechtskrümmung übergehend).
Der Wendepunkt (xw | yw) der Funktion f(x) = x3 ist also bei (0 | 0), am Koordinatenursprung:
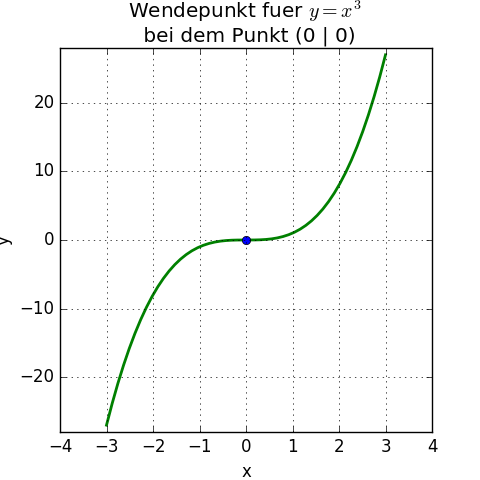
Maximale Anzahl der Wendepunkte
Die maximale Anzahl der Wendepunkte ergibt sich aus dem Grad der Funktion.
Die obige Funktion ist vom Grad 3 (weil ein x3 vorkommt), es gibt deshalb einen Wendepunkt (wenn die Funktion vom Grad 3 ist, ist die 2. Ableitung vom Grad 1: das x3 "schrumpft" durch das zweimalige Ableiten zu einem x1 bzw. x mit nur einer möglichen Lösung).
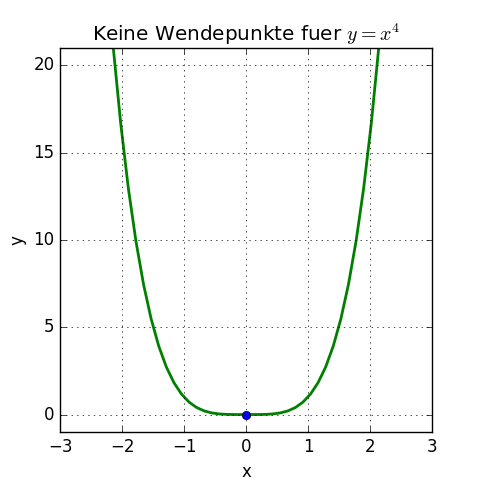
Eine Funktion vom Grad 4 (mit einem x4) kann maximal zwei Wendepunkte haben (oder nur einen oder gar keinen).
Die Funktion f(x) = x4 hat zum Beispiel keinen Wendepunkt (man müsste den Einschlag des Lenkrads nicht ändern, wenn man die Funktionskurve abfährt):