Lineare Gleichungen
Lineare Gleichung Definition
Eine lineare Gleichung hat die allgemeine Form: $m \cdot x + b = 0$
Die Variable x wird also mit einem Faktor / Koeffizienten multipliziert (der nicht 0 sein sollte, sonst fällt der x-Term weg) und eine Konstante b wird hinzuaddiert (oder subtrahiert: b kann auch eine negative Zahl wie -24 sein, b kann auch 0 sein).
Die Variable x kommt nur in der ersten Potenz vor, also nur als x (und nicht als zum Beispiel x2 – das wäre dann eine quadratische Gleichung).
Lineare Gleichungen sind einfach mit wenigen Umformungen zu lösen.
Beispiel
Beispiel: Lineare Gleichung mit einer Variablen lösen
Eine lineare Gleichung lautet:
$3 \cdot x - 24 = 0$
Gleichung nach x auflösen:
$3 \cdot x - 24 = 0 \qquad \vert +24$
$3 \cdot x = 24 \qquad \vert \div 3$
$x = 8$
Die einzige Lösung ist x = 8.
$3 \cdot 8 - 24 = 0$
Allgemein ist die Lösung:
$$x = \frac{-b}{m}$$
$$x = \frac{-(-24)}{3} = 8$$
In der Grafik sieht das so aus:
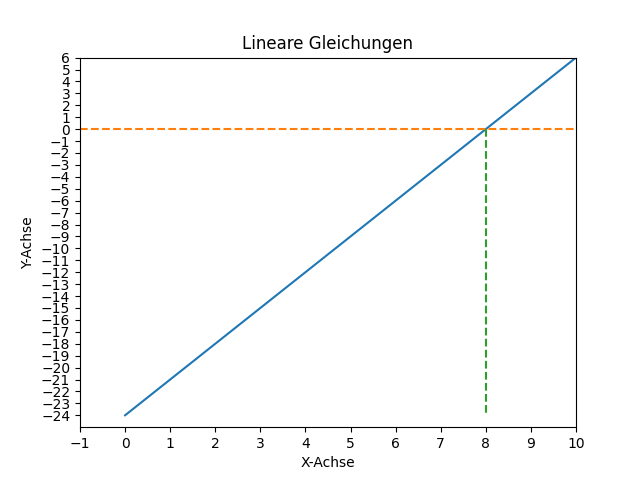
Da die Gleichung auf „= 0“ lautete, ist bei x = 8 die Nullstelle der Funktion f(x) = 3x - 24.
Mehrere Variablen
Lineare Gleichungen können auch mehrere Variablen haben, die allgemeine Form ist dann: $m \cdot x + n \cdot y + b = 0$
Auch hier werden die Variablen mit Koeffizienten multipliziert und die Terme werden dann aufaddiert. Die Variablen (hier x und y) dürfen aber zum Beispiel nicht multipliziert werden (also kein $x \cdot y$ in der Gleichung), sonst ist es keine lineare Gleichung.
Damit können lineare Gleichungssysteme gebildet werden.