Mittelwertsatz
Mittelwertsatz Definition
Ausgangspunkt für den Mittelwertsatz der Differentialrechnung: Eine Funktion f sei in einem abgeschlossenen Intervall [a, b] stetig (abgeschlossenes Intervall heißt: die Intervallgrenzen a und b gehören dazu) und im offenen Intervall ]a, b[ (das heißt ohne die Intervallgrenzen a und b) differenzierbar.
Dann gibt es mindestens einen x-Wert x*, für den gilt:
$$f'(x^*) = \frac{f(b) - f(a)}{b - a}$$
Die linke Seite der Gleichung ist die 1. Ableitung der Funktion f an der Stelle x*, das ist die Tangentensteigung.
Die rechte Seite der Gleichung ist die Sekantensteigung der Funktion f, das heißt die Steigung einer Geraden durch die Punkte a und b, die den Funktionsgraph schneidet.
Das bedeutet: Es gibt mindestens einen Punkt, an dem die Tangente parallel zur Sekante verläuft (parallel, da beide dieselbe Steigung haben).
Beispiel
Beispiel: Mittelwertsatz der Differentialrechnung
Die Funktion sei f(x) = x2 (das ist grafisch die Normalparabel).
Wir suchen uns 2 beliebige x-Werte, zum Beispiel x = 0 und x = 1 und berechnen dafür die Funktionswerte:
$$f(0) = 0^2 = 0$$
$$f(1) = 1^2 = 1$$
Das ergibt dann folgende 2 Punkte a und b auf dem Grafen (der erste Wert ist der x-Wert, der zweite Wert ist der y-Wert):
a: (0; 0)
b: (1; 1)
Die Sekantensteigung erhält man über die obige rechte Seite der Gleichung:
$$\frac{f(b) - f(a)}{b - a}$$
$$\frac{1 - 0}{1 - 0} = \frac{1}{1} = 1$$
Die Sekantensteigung ist also 1.
Als nächstes suchen wir ein x zwischen 0 und 1, für das die 1. Ableitung der Funktion (die Tangentensteigung) = 1 ist.
Die 1. Ableitung von f(x) = x2 ist f’(x) = 2x.
f’(x) = 2x = 1, das heißt x = 0,5.
f(0,5) = 0,52 = 0,25.
Die Tangentensteigung im Punkt (0,5; 0,25) ist 1 und damit gleich der Sekantensteigung.
Es gibt also hier mindestens einen Punkt, an dem die Tangente parallel zur Sekante verläuft (das ist natürlich kein Beweis des Mittelwertsatzes, nur eine beispielhafte Anwendung).
Als Grafik:
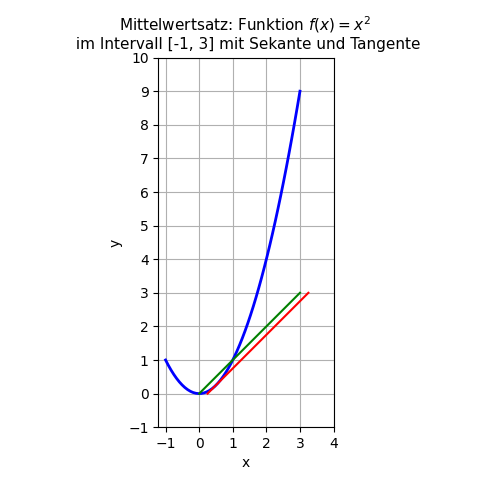
Die Sekante ist die linke, grüne Linie; die Tangente die rechte, rote Linie. Beide sind parallel zueinander.
(Anmerkung: oben eingezeichnet ist die Normalparabel im Intervall [-1, 3], um den Verlauf des Graphen anzudeuten; wir betrachten aber für den Mittelwertsatz im Beispiel das Intervall von 0 bis 1; innerhalb dieser Intervallgrenzen muss x* laut dem Mittelwertsatz liegen.)