Satz von Rolle
Satz von Rolle Definition
Der Ausgangspunkt für den Satz von Rolle ist (wie beim Mittelwertsatz): Eine Funktion f sei in einem abgeschlossenen Intervall [a, b] – einschließlich der Intervallgrenzen a und b – stetig und im offenen Intervall ]a, b[ – das heißt ohne die Intervallgrenzen a und b – differenzierbar.
Ist dann f(a) = f(b), das heißt, entspricht der Funktionswert an der Stelle a dem Funktionswert an der Stelle b (die Funktionswerte der beiden Intervallgrenzen liegen auf gleicher Höhe, die Sekante durch die Punkte ist waagrecht), gibt es mindestens einen x-Wert x* in dem offenen Intervall, für den gilt:
f'(x*) = 0.
Das bedeutet: Es gibt (mindestens) eine Stelle, an der die 1. Ableitung der Funktion f und damit die Steigung der Funktion gleich o ist (die Tangente ist waagrecht). Das kann ein Minimum oder eine Maximum sein.
Bildliche Vorstellung
Man kann sich den (gezeichneten) Umriss eines Hügels vorstellen, der Hügel beginnt bei a und endet bei b. Dazwischen liegt ein Maximum (des Hügels).
Oder: Man stellt sich den (gezeichneten) Umriss einer Grube im Boden vor, die bei a beginnt und bei b endet. Dazwischen liegt ein Minimum (der Grube).
Beispiel
Beispiel: Satz von Rolle
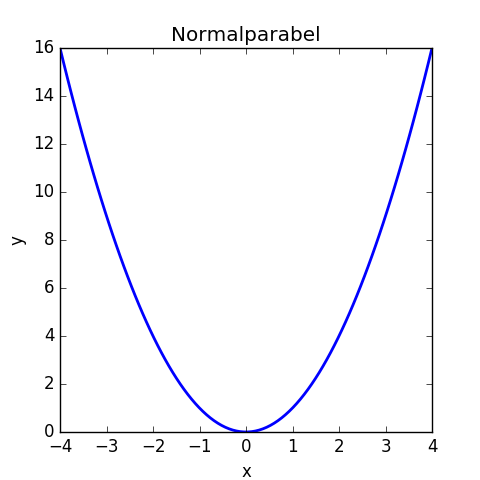
Wir betrachten die Funktion f(x) = x2 im Intervall von -2 bis 2.
Die Funktionswerte für x = -2 (a) und x = 2 (b) sind:
$$f(-2) = (-2)^2 = 4$$
$$f(2) = 2^2 = 4$$
f(a) ist also gleich f(b).
Es muss nun nach dem Satz von Rolle dazwischen mindestens eine Stelle geben, an der die 1. Ableitung der Funktion und damit die Steigung der Funktion gleich 0 ist.
Die 1. Ableitung der Funktion ist:
f’(x) = 2x.
Wir setzen die 1. Ableitung gleich 0:
2x = 0, das heißt x = 0.
Bei x = 0 ist hier die (einzige) Stelle im Intervall, an der die Steigung der Funktion gleich 0 ist.
Der Graph der Funktion ist die Normalparabel; man sieht, dass bei x = 0 ein Minimum vorliegt: