Normalparabel
Normalparabel Definition
Die Normalparabel ist der Graph der Funktion f(x) = x2 (Funktion, die jeder reellen Zahl ihre Quadratzahl zuordnet).
Eigenschaften
Die Normalparabel ist
- nach oben geöffnet,
- symmetrisch zur y-Achse und
- hat ihren Scheitelpunkt bzw. ihren tiefsten Punkt (Minimum) und ihre einzige Nullstelle im Koordinatenursprung (0, 0).
Normalparabel Wertetabelle
Die Wertetabelle der Normalparabel:
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| f (x) | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
Normalparabel verschieben
Die Normalparabel lässt sich verschieben:
- nach oben, zum Beispiel $f(x) = x^2 + 2$ (verschiebt die Normalparabel um 2 Einheiten nach oben)
- nach unten, zum Beispiel $f(x) = x^2 - 2$
- nach links, zum Beispiel $f(x) = (x + 2)^2$
- nach rechts, zum Beispiel $f(x) = (x - 2)^2$
Normalparabel zeichnen
Die Normalparabel sieht so aus:
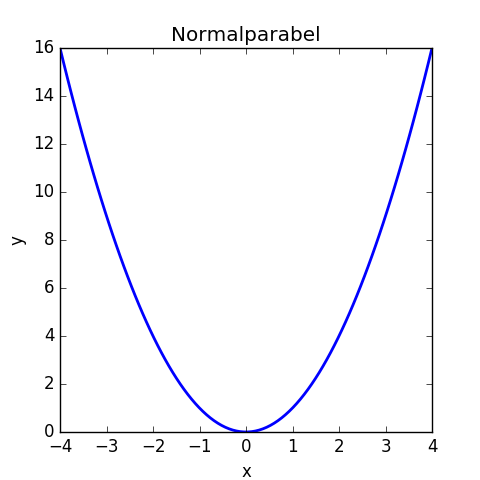
Wenn man die Punkte der Wertetabelle einträgt, kann man durch die 7 Punkte halbwegs zeichnen; mehr (Stütz-)Punkte wären besser.
Im Bereich der negativen x-Werte ist die Funktion streng monoton fallend, im Bereich der positiven x-Werte ist die Funktion streng monoton steigend.