Polstelle
Polstelle Definition
Eine Polstelle einer Funktion ist eine Definitionslücke (Stelle, an der die Funktion nicht definiert ist), in deren Nähe die y-Funktionswerte gegen plus oder minus unendlich laufen.
Der Funktionsgraph kann nicht durchgehend gezeichnet werden, sondern hat eine Unterbrechung bei der Definitionslücke.
Beispiel
Beispiel Polstelle
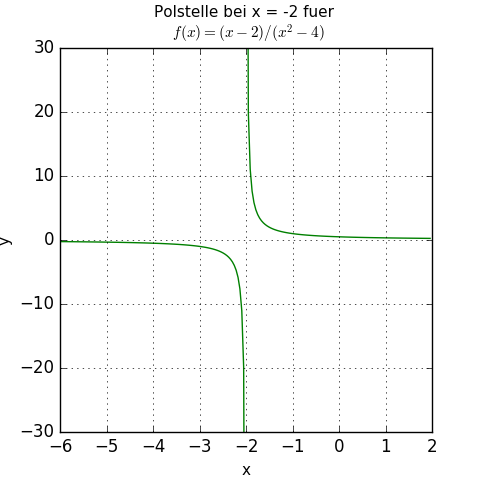
Die Funktion sei f(x) = (x - 2) / (x2 - 4).
#1: Nullstellen des Nenners bzw. Definitionslücken bestimmen
Man darf nicht durch 0 teilen, deshalb darf der Nenner nicht 0 sein.
Für x = -2 wäre der Nenner jedoch 0 (-22 - 4 = 4 - 4 = 0) und für x = 2 ebenso (22 - 4 = 4 - 4 = 0).
Es gibt also 2 Definitionslücken: -2 und 2.
#2: Nullstellen des Nenners auch Nullstellen des Zählers?
Als nächstes prüft man, ob die Nullstellen des Nenners auch welche des Zählers sind.
Für x = -2 ist das nicht der Fall: -2 - 2 = - 4. Hier liegt eine Polstelle vor.
Für x = 2 ist das der Fall: 2 - 2 = 0. Deshalb liegt hier eine sogenannte hebbare Definitionslücke vor. Die Nullstelle lässt sich durch Kürzen entfernen, dadurch wird die Lücke geschlossen:
f(x) = (x - 2) / (x2 - 4) kann man – unter Anwendung der 3. binomischen Formel im Nenner – auch als f(x) = (x - 2) / [(x - 2) × (x + 2)] schreiben und dann gekürzt als 1 / (x +2).
Für x = 2 ist die Definitionslücke jetzt geschlossen.
Mit einer Beispielzahl (zum Beispiel x = 5) gezeigt:
f(5) = (5 - 2) / (52 - 4) = 3 / 21 = 1/7.
f(5) = 1 / (5 + 2) = 1/7.
In der Grafik sieht man das Verhalten der Funktion bei der Polstelle: