Monotonieverhalten
Monotonieverhalten Definition
Das Monotonieverhalten einer Funktion beschreibt, ob bzw. in welchen Bereichen die untersuchte Funktion steigt oder fällt.
(Streng) montoton steigend und (streng) montoton fallend
Die Funktion kann
- streng monoton steigen: für steigende (in die Funktion eingesetzte) x-Werte steigen die Funktionswerte / y-Werte ebenfalls; einfaches Beispiel: f(x) = 2x ("Verdopplungsfunktion"); für positive x steigen die y-Werte: für x = 1 ist y = 2, für x = 2 ist y = 4 usw.; gezeichnet ergibt das eine aufsteigende Gerade. Das "streng" lässt man weg, wenn es auch konstante Phasen gibt; eine hochlaufende Rampe wäre streng monoton steigend, eine Treppe nur monoton steigend;
- streng monoton fallen: für steigende x-Werte fallen die y-Werte; die Funktion f(x) = -2x wäre zum Beispiel für positive x streng monoton fallend: für x = 1 wäre y = -2, für x = 2 wäre y = -4 usw.; gibt es wiederum konstante Phasen, entfällt das "streng";
- konstant bleiben, zum Beispiel f(x) = 2. Für alle x ist der Funktionswert konstant 2.
Monotoniekriterium
Ist die erste Ableitung f'(x) einer (stetigen) Funktion > 0, ist die Funktion (in dem jeweiligen Bereich) streng monoton steigend.
Die 1. Ableitung der Funktion f(x) = 2x ist f'(x) = 2. Das heißt, die 1. Ableitung ist immer 2 und damit immer positiv, egal welche x-Werte man einsetzt. Die Funktion ist streng monoton steigend.
Ist die erste Ableitung f'(x) einer (stetigen) Funktion < 0 (also negativ), ist die Funktion (in dem jeweiligen Bereich) streng monoton fallend.
Die 1. Ableitung der Funktion f(x) = -2x ist f'(x) = -2. Das heißt, die 1. Ableitung ist immer -2 und damit immer negativ. Die Funktion ist streng monoton fallend.
Für <= 0 statt < 0 oder >= 0 statt > 0 entfällt das "streng".
Alternative Begriffe: Monotonie.
Monotonie Beispiel
Beispiel: Funktion auf Monotonie untersuchen
Die Funktion sei:
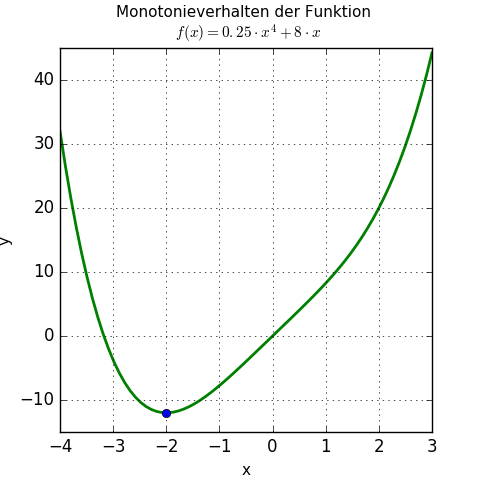
$$f(x) = \frac{1}{4} \cdot x^4 + 8 \cdot x$$
Die 1. Ableitung bilden:
$$f'(x) = x^3 + 8$$
Für einen x-Wert von zum Beispiel -3 wäre die 1. Ableitung $f'(-3) = (-3)^3 + 8 = -19$ und damit negativ.
Für einen x-Wert von zum Beispiel 3 wäre die 1. Ableitung $f'(3) = (3)^3 + 8 = 35$ und damit positiv.
Um die monoton steigenden und fallenden Bereiche abzugrenzen, wird die 1. Ableitung gleich 0 gesetzt:
$$x^3 + 8 = 0$$
$$x^3 = -8$$
$$x = -2$$
Für x < -2 ist f'(x) < 0, das heißt, die Funktion ist streng monoton fallend.
Für x > -2 ist f'(x) > 0, das heißt, die Funktion ist streng monoton steigend.
Das kann man im Funktionsgraphen gut sehen: