Quadratische Ungleichungen
Quadratische Ungleichungen Definition
Eine quadratische Ungleichung sieht in ihrer allgemeinen Form so aus:
$$x^2 + px + q > 0$$ oder
$$x^2 + px + q < 0$$
Dabei können p oder q auch negative Zahlen sein.
Beispiel
Beispiel: Quadratische Ungleichung lösen
Im Beispiel zur p-q-Formel gab es eine quadratische Gleichung
$$2x^2 + 2x - 12 = 0$$
Diese soll nun als quadratische Ungleichung formuliert werden, zum Beispiel:
$$2x^2 + 2x - 12 > 0$$
Die beiden Nullstellen der Gleichung waren 2 und -3, die Linearfaktordarstellung der Gleichung war:
$$2 \cdot (x - 2) \cdot (x + 3) = 0$$
Jetzt kann man sich überlegen, wann die linke Seite der Gleichung nicht gleich 0, sondern größer als 0 ist. Dazu müssen beide Faktoren, also (x - 2) und (x + 3) gleichzeitig größer oder gleichzeitig kleiner 0 sein.
Also entweder
- x > 2 und x > -3 (das heißt, x muss größer 2 sein) oder
- x < 2 und x < -3 (das heißt, x muss kleiner -3 sein).
Die Lösungsmenge umfasst dann den Bereich x < -3 oder x > 2.
Hier die Grafik dazu:
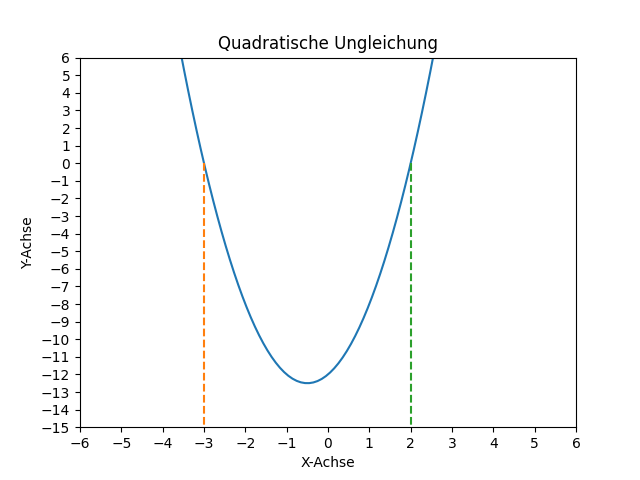
Man sieht, dass die Funktion für die Bereiche x < -3 und x > 2 oberhalb der Nulllinie auf der y-Achse liegt und für die Werte dazwischen unter der Nulllinie.