Sinussatz
Sinussatz Definition
Der Sinussatz gilt allgemein in Dreiecken.
Formel
Der Sinussatz lautet:
$$\frac{a}{sin(\alpha)} = \frac{b}{sin(\beta)} = \frac{c}{sin(\gamma)}$$
Dabei sind a, b und c die Längen der Seiten des Dreiecks und $\alpha$, $\beta$ und $\gamma$ sind die jeweils gegenüberliegenden Winkel im Dreieck (der Winkel $\alpha$ liegt a gegenüber, der Winkel $\beta$ liegt b gegenüber und der Winkel $\gamma$ liegt c gegenüber).
Beispiel
Beispiel: Sinussatz
Wir greifen das Dreieck aus dem Sinus-Beispiel auf:
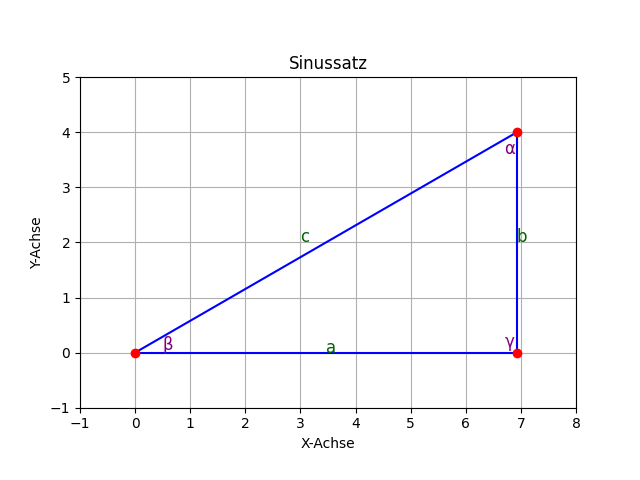
Die Seite a hat eine Länge von 6,928 cm, die Seite b hat eine Länge von 4 cm und die Seite c hat eine Länge von 8 cm.
Für die Winkel gilt:
- der a gegenüberliegende Winkel $\alpha$ hat 60 Grad,
- der b gegenüberliegende Winkel $\beta$ hat 30 Grad und
- der c gegenüberliegende Winkel $\gamma$ hat 90 Grad (wir haben hier also ein rechtwinkliges Dreieck; das muss aber nicht sein, der Sinussatz gilt für alle Dreiecke).
Sinussatz anwenden
$$\frac{a}{sin(\alpha)} = \frac{6,928}{sin(60^\text{o})} = 8$$
$$\frac{b}{sin(\beta)} = \frac{4}{sin(30^\text{o})} = 8$$
$$\frac{c}{sin(\gamma)} = \frac{8}{sin(90^\text{o})} = 8$$
(Für die Sinusberechnung von zum Beispiel 60 Grad die 60 in den Taschenrechner eingeben und die SIN-Taste drücken).