Verbindungsvektor
Verbindungsvektor Definition
Hat man zum Beispiel zwei Punkte A und B:
- A mit den Koordinaten A (2, 3), also vom Ursprung aus 2 cm (oder eine andere Einheit) auf der x-Achse nach rechts und 3 cm auf der y-Achse nach oben und
- B mit den Koordinaten B (4, 5), also vom Ursprung aus 4 cm auf der x-Achse nach rechts und 5 cm auf der y-Achse nach oben,
heißt der Vektor, der die beiden Punkte A und B verbindet, Verbindungsvektor bzw. Richtungsvektor.
Schreibweise:
$$\overrightarrow {AB}$$
Verbindungsvektor berechnen
Der Verbindungsvektor von A nach B lässt sich berechnen, indem man vom Ortsvektor zum Punkt B den Ortsvektor zum Punkt A abzieht:
$$\overrightarrow {AB} = \vec b - \vec a = \begin{pmatrix}4 \\ 5 \end{pmatrix} - \begin{pmatrix}2 \\ 3 \end{pmatrix}$$
$$= \begin{pmatrix}4 - 2 \\ 5 - 3 \end{pmatrix} = \begin{pmatrix}2 \\ 2 \end{pmatrix}$$
Das Ergebnis bedeutet, dass man vom Punkt A aus 2 cm nach rechts und 2 cm nach oben gehen muss, um zum Punkt B zu kommen.
Man kann mit diesen Vektordaten einen Verbindungspfeil zeichnen, der "nordwestlich" zeigt.
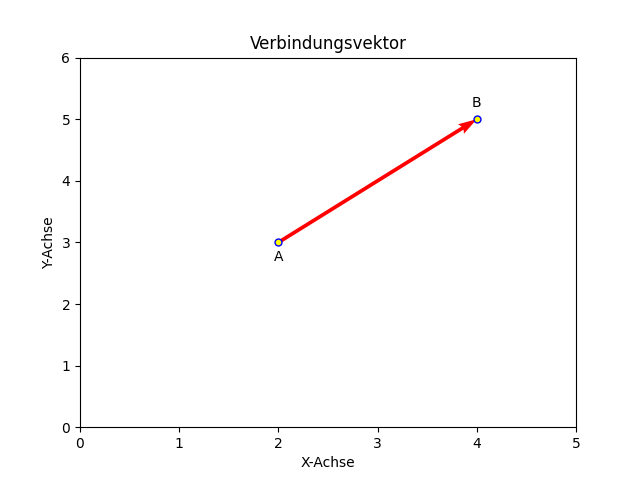
Der Betrag des Verbindungsvektors ist der Abstand zwischen den beiden Punkten A und B.
$$\vert \overrightarrow {AB} \vert = \sqrt{2^2 + 2^2}$$
$$= \sqrt{4 + 4} = \sqrt{8} = 2,83 \, cm$$
Umgekehrt kann auch der Verbindungsvektor von B nach A berechnet werden, indem man vom Ortsvektor zum Punkt A den Ortsvektor zum Punkt B abzieht:
$$\overrightarrow {BA} = \vec a - \vec b = \begin{pmatrix}2 \\ 3 \end{pmatrix} - \begin{pmatrix}4 \\ 5 \end{pmatrix}$$
$$= \begin{pmatrix}2 - 4 \\ 3 - 5 \end{pmatrix} = \begin{pmatrix}-2 \\ -2 \end{pmatrix}$$
Verbindungsvektoren lassen sich analog auch im dreidimensionalen Raum bestimmen.