Kovarianz
Kovarianz Definition
Die Kovarianz misst den Zusammenhang zwischen zwei Merkmalen bzw. Variablen (zum Beispiel den Zusammenhang zwischen Körpergröße und Gewicht) und prüft, ob ein linearer Zusammenhang vorliegt.
Die Kovarianz setzt, da ihre Formel bzw. Berechnung auf arithmetischen Mittelwerten basiert, metrische (zumindest intervallskalierte) Merkmale voraus.
Formel
Die Kovarianz-Formel (mit Cov für Covariance) lautet:
$$Cov (x, y) = \frac{\sum_{i = 1}^n (x_i - \bar x) \cdot (y_i - \bar y)}{n}$$
Dabei sind xi und yi die jeweiligen Werte der beiden Variablen, $\bar x$ und $\bar y$ der arithmetische Mittelwert (Durchschnitt) von x bzw. y, und n ist die Anzahl der untersuchten Merkmalsträger.
Die Formel in Worten
Für die Berechnung der Kovarianz werden also
- für beide Merkmale jeweils für alle Merkmalswerte die Differenz zwischen der jeweiligen Merkmalsausprägung (Messwert) und dem arithmetischen Mittelwert des Merkmals gebildet,
- die Differenzen / Abweichungen anschließend multipliziert (ergibt die sogenannten Abweichungsprodukte) und
- dann alle Abweichungsprodukte aufaddiert und durch die Anzahl der Merkmalsträger bzw. Messungen geteilt.
Abweichende Formel bei Stichproben
Die obige Formel gilt für den Fall, dass man Daten einer vollständigen Grundgesamtheit analysiert (wie im Beispiel unten bei den 3 Milchkühen).
Hat man hingegen die Daten einer Stichprobe, wird nicht durch n geteilt, sondern durch (n - 1); bei 3 Stichproben also durch (3 - 1) = 2.
Die Formel für diese empirische Kovarianz lautet dann mit entsprechend geändertem Nenner:
$$Cov (x, y) = \frac{\sum_{i = 1}^n (x_i - \bar x) \cdot (y_i - \bar y)}{n - 1}$$
Beispiel
Kovarianz berechnen
Angenommen, die 3 Milchbauern Anton, Bernd und Claus haben folgende Anzahl von Kühen und folgende tägliche Milchmengen.
| Anton | Bernd | Claus | |
|---|---|---|---|
| Anzahl der Milchkühe | 1 | 2 | 3 |
| Tägliche Milchproduktion (Liter) | 30 | 60 | 90 |
| Abweichung der Anzahl der Kühe vom Durchschnitt | -1 | 0 | 1 |
| Abweichung der Milchproduktion vom Durchschnitt | -30 | 0 | 30 |
| Produkt der Abweichungen | 30 | 0 | 30 |
Dann ist das arithmetische Mittel der Anzahl der Kühe ( 1 + 2 + 3) / 3 = 2 und das arithmetische Mittel der Milchleistung (30 + 60 + 90 Liter) / 3 = 60 Liter.
Gibt es einen linearen Zusammenhang zwischen der Anzahl der Kühe und der Milchproduktion? (der – lineare – Zusammenhang ist hier natürlich sehr offensichtlich und ist auch sofort aus dem dazugehörigen Streudiagramm erkennbar)
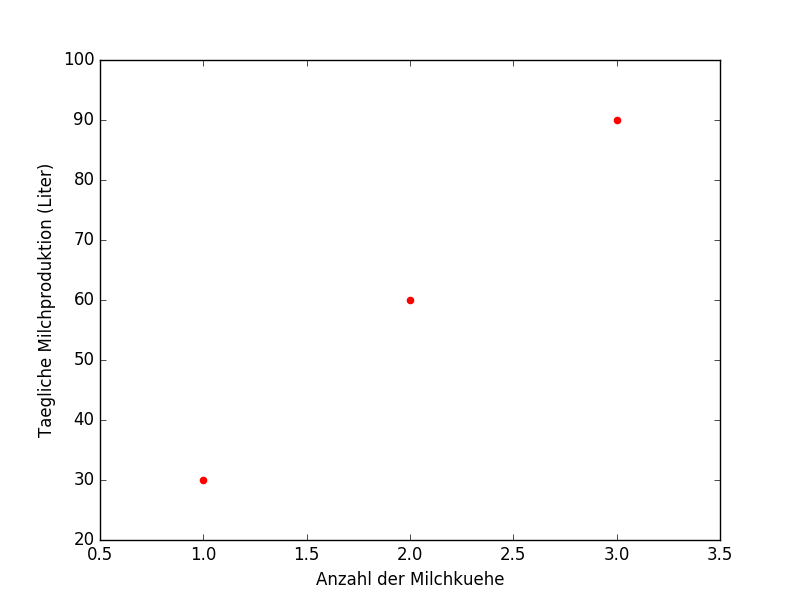
Berechnung Kovarianz
Die 3 Abweichungsprodukte werden aufaddiert: 30 + 0 + 30 = 60; anschließend durch die Anzahl der Merkmalsträger (3 Milchbauern) geteilt: 60 / 3 = 20.
Bei den 3 betrachteten Milchbauern soll es sich hier um die gesamte Grundgesamtheit handeln; wird hingegen eine Stichprobe betrachtet, ist wie oben beschrieben nicht durch die Anzahl der Merkmalsträger, sondern durch (Anzahl der Merkmalsträger - 1) zu teilen (das wären hier 3 - 1 = 2).
Das Produkt der Abweichungen für Anton ergibt sich daraus, dass die negative Abweichung von -1 mit der negativen Abweichung von - 30 (Liter) multipliziert wird; dies ergibt +30.
Als vollständige Formel:
Cov = [ (1 - 2) × (30 - 60) + (2 - 2) × (60 - 60) + (3 - 2) × (90 - 60) ] / n = (30 + 0 + 30) / 3 = 60/3 = 20.
Interpretation: Positive Kovarianz
Positive Werte der Kovarianz bedeuten, dass hohe Werte des einen Merkmals (hier: Milchproduktion) mit hohen Werten des anderen Merkmals (hier: Anzahl der Kühe) einhergehen (und umgekehrt).
Probleme der Kovarianz
Bei der Kovarianz werden hier Stückzahlen mit Litern multipliziert; die Größe bzw. Höhe der Kovarianz ist – im Gegensatz zur Richtung / zum Vorzeichen – schlecht interpretierbar.
Zudem würde eine Änderung der Messeinheiten (zum Beispiel Gallonen statt Liter) zu anderen Werten der Kovarianz führen.
Die Kovarianz wird deshalb oft nur als Ausgangspunkt für die Berechnung weiterer Korrelationskoeffizienten (zum Beispiel Pearson-Korrelationskoeffizient) genutzt.
Unkorreliertheit
Ist die Kovarianz gleich Null, liegt keine Korrelation vor (und es muss nicht weitergerechnet werden). Man sagt dann, die beiden Merkmale sind unkorreliert.