Sattelpunkt
Sattelpunkt Definition
Ein Sattelpunkt einer Funktion (auch Terrassenpunkt genannt) ist ein Wendepunkt (ein Punkt, in dem sich das Krümmungsverhalten ändert) mit der zusätzlichen Bedingung, dass die Steigung der Funktion (also die 1. Ableitung) an dem Wendepunkt 0 ist.
Beispiel
Beispiel: Sattelpunkt berechnen
Hier soll das Beispiel zum Wendepunkt fortgeführt werden:
Die Funktion war f(x) = x3.
Es wurden bereits die ersten drei Ableitungen der Funktion berechnet:
Die 1. Ableitung ist f'(x) = 3x2.
Die 2. Ableitung ist f''(x) = 6x. Setzt man diese 2. Ableitung gleich 0 (also 6x = 0), ergibt dies x = 0.
Die 3. Ableitung f'''(x) ist 6. Da die 3. Ableitung an der Stelle 0, also f'''(0) = 6 und damit ungleich 0 war, lag ein Wendepunkt vor.
Nun wird der Wendepunkt x = 0 in die 1. Ableitung eingesetzt: f'(0) = 3 × 02 = 3 × 0 = 0.
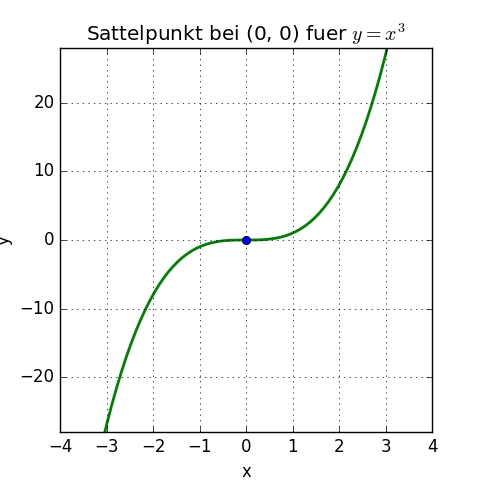
Da die Steigung des Wendepunkts 0 ist, liegt im Wendepunkt x = 0 und y = 03 = 0, also im Koordinatenursprung (0, 0), ein Sattelpunkt vor.
Der Sattelpunkt in der Grafik:
Kein Sattelpunkt
Wandelt man die Funktion etwas ab in f(x) = x3 + x, liegt bei (0, 0) zwar ein Wendepunkt vor (das Krümmungsverhalten ändert sich), aber kein Sattelpunkt (man "rutscht" im Punkt (0, 0) schräg ab, während man beim obigen Sattelpunkt "waagrecht sitzen" konnte):
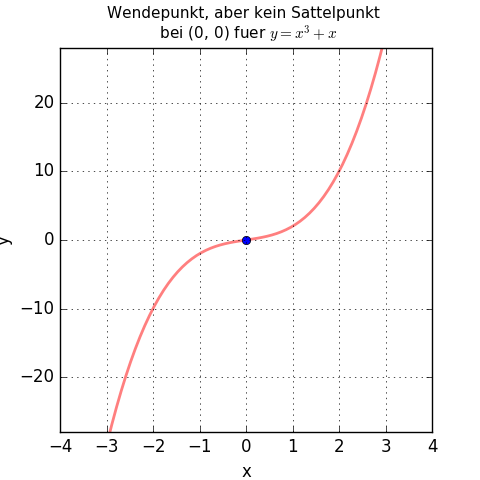
Die 1. Ableitung dieser abgewandelten Funktion ist f'(x) = 3x2 + 1.
An der Stelle x = 0, bei der wiederum ein Wendepunkt vorliegt, ist sie deshalb f'(0) = 3 × 02 + 1 = 1 und damit ungleich 0. Die Steigung der Funktion ist also hier nicht 0.