Wendetangente
Wendetangente Definition
Eine Wendetangente ist eine Tangente durch einen Wendepunkt einer Funktion, das heißt, eine Gerade, welche die Funktionskurve im Wendepunkt berührt.
Die Wendetangente wird durch eine Geradengleichung beschrieben, dafür werden
- der Wendepunkt und
- die Steigung im Wendepunkt benötigt.
Beispiel
Die Funktion sei f(x) = x3.
Wendepunkt
Für die Funktion war bereits ein Wendepunkt berechnet worden; dieser lag bei x = 0 und y = f(0) = 03 = 0.
Der Wendepunkt (xw | yw) der Funktion f(x) = x3 ist also bei (0 | 0), am Ursprung des Koordinatensystems.
Hier nochmals die Grafik, die den Wendepunkt zeigt:
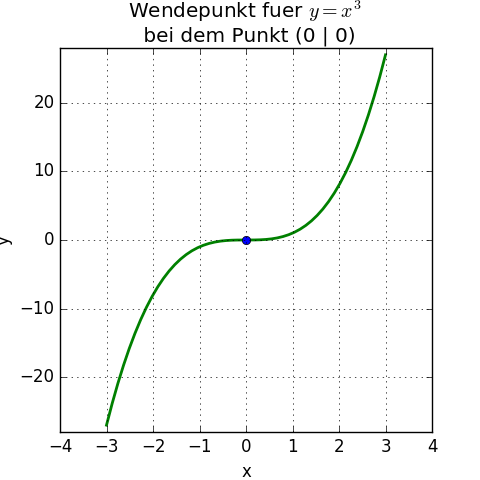
Zur Erinnerung: im Wendepunkt ändert der Graph sein Krümmungsverhalten: im Bereich der negativen x der Grafik würde ein Autofahrer das Lenkrad rechts einschlagen bis zum Nullpunkt, ab da (im Bereich der positiven x) dann links einschlagen.
Allgemein: eine Rechtskurve geht in eine Linkskurve über oder umgekehrt eine Linkskurve in eine Rechtskurve.
Steigung im Wendepunkt
Die Steigung m im Wendepunkt erhält man, indem in die 1. Ableitung der Funktion der Wendepunkt xw eingesetzt wird.
Die 1. Ableitung der Funktion f(x) = x3 ist f'(x) = 3x2.
Für den Wendepunkt mit xw = 0:
f'(0) = 3 × 02 = 3 × 0 = 0.
Die Steigung m der Wendetangente ist 0.
Funktionsgleichung der Wendetangente
Die Gleichung der Wendetangente t(x) lautet allgemein:
$$t(x) = m \cdot (x - x_w) + y_w$$
Dabei ist $m$ die Steigung und $x_w$ und $y_w$ sind die Koordinaten des Wendepunktes.
Die Gleichung der Wendetangente t(x) mit den eingesetzten Zahlen für Wendepunkt und Steigung:
$$t(x) = 0 \cdot (x - 0) + 0 = 0$$
Die Wendetangente ist hier also eine Gerade, die waagerecht auf der x-Achse des Koordinatensystems verläuft.
Hier liegt ein Spezialfall vor: ein Sattel- bzw. Terrassenpunkt.
Fazit
Man kann an eine Funktionskurve in der Regel unzählige Tangenten in unzähligen Punkten anlegen. Eine Wendetangente ist eine Tangente durch einen bestimmten Punkt, nämlich einen Wendepunkt.
Die Wendetangente hat an dem Wendepunkt dieselbe Steigung wie die Funktion.