Dritte Ableitung
Dritte Ableitung Definition
Die 3. Ableitung ist eine Ableitung der 2. Ableitung einer Funktion.
Die 3. Ableitung wird mit 3 Strichen gekennzeichnet: f’’’(x).
Beispiel
Beispiel 3. Ableitung
Für die Potenzfunktion f(x) = x3 ist die 1. Ableitung f’(x) = 3x2 (siehe Potenzfunktion ableiten).
Zur Erinnerung: Eine Potenzfunktion wird abgeleitet, indem man den Exponenten (im Beispiel 3) als Faktor vor den Term setzt und anschließend den Exponenten um 1 reduziert (im Beispiel von 3 auf 2).
Durch Ableitung dieser 1. Ableitung erhält man die 2. Ableitung f’’(x) = 6x (wiederum Ableitung einer Potenzfunktion).
Der Exponent 2 wird wieder als Faktor vor den Term gesetzt (2 × 3 = 6) und anschließend wird der Exponent erneut um 1 reduziert (von 2 auf 1 und das „hoch 1“ schreibt man dann nicht mehr da x1 = x ist).
Leitet man diese 2. Ableitung erneut ab, erhält man die 3. Ableitung f’’’(x) = 6 (siehe Variable mit Faktor ableiten).
Bedeutung
Die 3. Ableitung wird unter anderem genutzt, um für einen Wendepunkt zu zeigen, ob
- ein Rechts-Links-Wendepunkt vorliegt (von einer Rechts- in eine Linkskrümmung übergehend; man schlägt das Lenkrad bis zum Wendepunkt rechts und ab da dann links ein), die 3. Ableitung ist hier im Wendepunkt > 0, oder
- ob ein Links-Rechts-Wendepunkt vorliegt (von einer Links- in eine Rechtskrümmung übergehend), die 3. Ableitung ist hier im Wendepunkt < 0.
Siehe das Beispiel zum Wendepunkt, das auf der hier verwendeten Funktion f(x) = x3 beruht.
Da hier die 3. Ableitung für alle x gleich f’’’(x) = 6 und damit > 0 ist, ist sie auch für den Wendepunkt bei x = 0 größer 0 und es liegt ein Rechts-Links-Wendepunkt vor.
Hier nochmals die Grafik der Funktion:
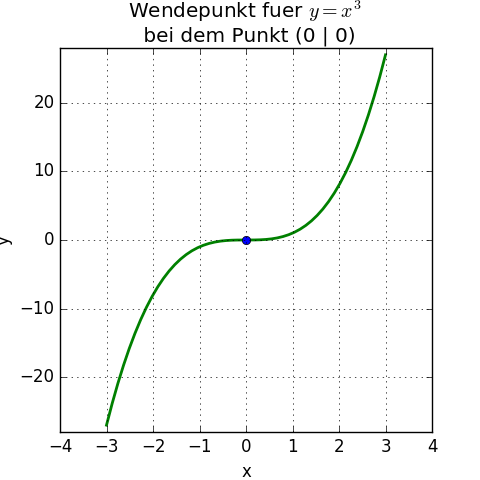
Dritte Ableitung gleich 0
Ist die 3. Ableitung = 0 (was im Beispiel für kein x der Fall ist, da die 3. Ableitung immer konstant 6 ist), kann ein Sattelpunkt vorliegen (eine Wendepunkt, bei dem die Steigung der Funktion, also die 1. Ableitung, 0 ist).