Grenzwert
Grenzwert Definition
Der Grenzwert einer Funktion ist die Zahl, der sich die y-Werte einer Funktion nähern, wenn man die x-Werte einem bestimmten Wert (z.B. dem Unendlichen) annähert.
Beispiel: Verhalten im Unendlichen
Als Frage: "Welchem Wert nähert sich die Funktion f(x) = 1/x, wenn man x gegen plus unendlich laufen lässt?"
Mathematisch (mit lim für limes, lateinisch für Grenzwert):
$$\lim\limits_{x\to\infty} \frac{1}{x} = 0$$
Für x = 10, wäre der Funktionswert 1/10, für x = 100 dann 1/100, für x = 1.000 dann 1/1.000 u.s.w. Nähert man x plus unendlich an, strebt der Funktionswert gegen Null, der Grenzwert ist 0.
Das kann man im Funktionsgraphen gut sehen:
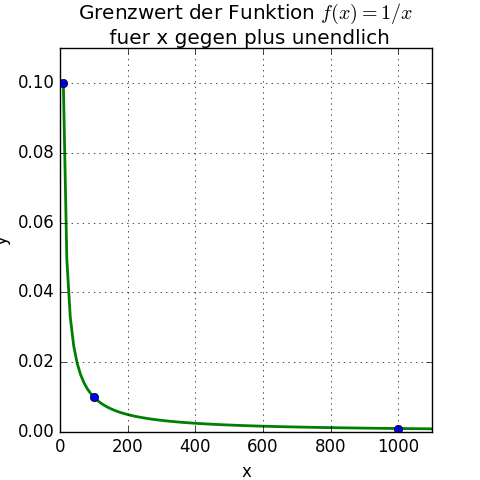
Der Grenzwert für x gegen minus unendlich strebt ebenfalls gegen 0 (nur von der anderen Seite).
Wie sich eine Funktion für x gegen plus unendlich und minus unendlich verhält, heißt auch Globalverhalten.
Nicht jede Funktion hat einen Grenzwert.
Alternative Begriffe: Funktionsgrenzwert, mathematischer Grenzwert.
Weitere Grenzwertberechnungen
Die Variable x muss nicht gegen unendlich laufen, sie kann auch gegen 0 oder jede andere Zahl laufen.
Grenzwert für x gegen 0
Beispiel: Limes für x gegen 0
Die Funktion sei:
$$f(x) = \frac{2x + x^2}{x} = \frac{x(2 + x)}{x}$$
Für x = 0 ist die Funktion nicht definiert (da man nicht durch 0 teilen darf), ansonsten kürzt sich x raus und für den Grenzwert gilt:
$$\lim\limits_{x\to 0} = \frac{x(2 + x)}{x} = \lim\limits_{x\to 0} 2 + x = 2$$
Mann kann sich x als sehr kleine Zahl nahe Null vorstellen, z.B. 0,00001, um auf den Grenzwert zu kommen.
Grenzwert für x gegen eine beliebige Zahl
Beispiel: Limes für x gegen 2
Die Funktion sei:
$$f(x) = x + 3$$
Für den Grenzwert gilt:
$$\lim\limits_{x\to 2} x + 3 = 5$$
Mann kann sich x wieder als Zahl sehr nahe an 2 vorstellen, z.B. 1,99999, um auf den Grenzwert zu kommen.